AP Physics 2 – Online lesson Battery EMF and Internal Resistance

Access the online HTML5 simulation PhET Circuit Construction Kit: DC – Virtual Lab.  Use this lesson in conjunction with the online notes. 

1. Set up a simple circuit with a battery, an ammeter, and a resistor as shown below.  Click on the battery and change its voltage to 10 volts, click on the resistor and change its resistance to 5 ohms.  Use options:  Conventional current and Values.

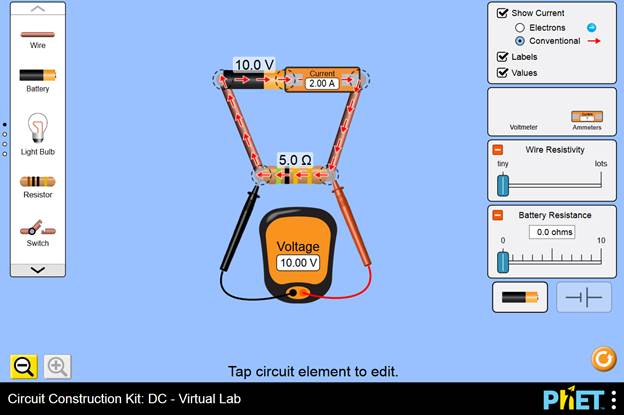
(This screenshot shows the result of clicking on the resistor and adjusting.)

2. Use the voltmeter to measure the voltage across the battery and across the resistor.

3. Try measuring the voltage across one of the wires.  Why is it zero?

4. Now connect the voltmeter once again across the resistor.  Increase the Wire Resistivity until the voltage of the resistor is only 5 volts.  Is the battery still 10 volts?  Measure it!  Where is the “missing voltage”?  Measure the voltage across each wire. 

5. Experiment with the Wire Resistivity and measure the voltages – does the sum of the voltages outside the battery always equal 10 volts?

6. Now reset the Wire Resistivity to tiny.  Adjust the Battery Resistance to 1.0 ohms and measure all the voltages.  Experiment with the Battery Resistance and repeat.

7. Continue to experiment with Battery Resistance but also try changing the voltage of the battery.  For example what happens if you double the battery voltage to 20 volts. 

8. Measuring the battery voltage by connecting to its positive and negative terminals is called the “terminal voltage” of the battery.  Whenever there is a current through the battery this voltage will be less than the battery’s “rating”, which is referred to as the EMF.

9. Experiment with all of the parameters in the program to determine how the difference in the EMF and the terminal voltage depends on the internal resistance and current.  How can the behavior of the battery be modeled?

10. See the online notes for a summary of ideas.

11. Try working the online examples problems 6 – 8.  Answers to check yourself:

6. a. 2.97 V, 58.8 mW
b. 3²/150 = 60 mW – ideally resistor would dissipate this power, but internal resistance lowers the “available” voltage and power
c. The “lost” voltage and power are associated with the internal resistance:  0.0297 V, 0.588 mW.  The sum of this power and that found in part (a) is equal to the power associated with emf P = VI = 59.4 mW = 58.8 mW + 0.588 mW.

7. a. 2.99 V
b. 2.94 V
c. series circuit is more efficient because the internal resistance wastes energy as heat more rapidly the greater the current, as is the case in the parallel circuit.

8. a. 6.32 W dissipated by the three resistors if the cell is connected across the 10 ohm resistor.
    (The triangle of resistors is equivalent to 8.33 ohms – 20 ohms in series with 30 ohms to
    form 50 ohms parallel to 10 ohms!)
b. 10 ohm:  7.26 V, 0.726 A 
    20 ohm:  2.90 V, 0.145 A  
    30 ohm:  4.36 V, 0.145 A