WooHoo Way Fun Wave Stuff
Unless stated otherwise, for all problems given below use: speed of light c = 3.00 × 108 m/s and speed of sound in air v = 343 m/s.
1. A tuning fork vibrates at 880 Hz. What will be the wavelength and period of the sound produced?
2. (a) Determine the wavelength of FM station 102.1 MHz. (b) Determine the wavelength of AM station 1340 kHz.
3. A wave with period 0.078 s passes from a steel spring, where v = 2.0 m/s, to a bronze spring, where v = 3.5 m/s. (a) Determine the frequency and wavelength in the steel spring. (b) Determine the frequency and wavelength in the bronze spring.
4. Determine the frequency for a laser that produces light with wavelength 633 nm.
5. A microwave oven operates at frequency 2450 MHz. Determine the wavelength of the radiation that heats the food.
6. The source of a wave affects which wave parameters?
7. The medium through which a wave travels affects which parameters?
8. What is the medium for electromagnetic radiation?
9. What is the difference between longitudinal and transverse waves? Which of these is sound? Which of these is light? Which of these is ultraviolet?
10. A bird on a horizontal wire bobs up and down 7.00 times in 3.00 seconds producing a wave in the wire. A second bird is located 24.0 m away on the same wire. The second bird is observed to start bobbing up and down 0.857 s after the first bird started bobbing. The wire has mass per length equal to 0.150 kg/m. (a) Determine the speed of the wave. (b) Determine the tension in the wire. (c) frequency of the wave. (d) Determine the wavelength of the wave. (e) Determine the period of the second bird’s oscillation. (f) Determine whether the two bobbing birds are in phase or out of phase as they bob up and down.
11. Graph the following wave on your calculator using equations of the form y = Asin(Bx): a sinusoidal wave with speed 35 m/s, amplitude 6.5 cm, and frequency 25 Hz. (a) On the disturbance versus time graph determine the amount of disturbance at t = 0.050 s. (b) On the disturbance versus distance graph determine the amount of disturbance at d = 1.0 m.
12. A certain sound wave is
described by the equation y(x) = 3 sin(20x) + sin(80x),
where x = distance in meters and y = pressure change in
milliPascals.
(a) Determine the wavelength of the wave. (b) Determine the amplitude of the
wave. (c) Determine the frequency of the wave. (d) Determine the period of
the wave.
13. Two speakers produce sound waves at the same time: wave A has wavelength 14.0 cm and amplitude 0.50 mPa, wave B has wavelength 14.0 cm and amplitude 0.30 mPa. Determine the wavelength and amplitude of the superposition of these two waves and state the type of interference for two cases: (a) the two waves are exactly in phase, (b) the two waves are exactly out of phase.
14. A certain skyscraper is 440 m tall and is found to sway back and forth with a period of 10.0 seconds. A simple model of this phenomenon would be to assume the building is like a huge standing wave where the base of the building is like a node and the top of the building is like an anitnode. If this is the case what is the speed of waves traveling up and down the building?
15. A drainage pipe is open at both ends and is 4.00 m long. At certain times the wind blows just right and the pipe is heard to whistle. Determine the most probable frequencies of the pipe’s whistling sound.
16. An organ pipe involves standing waves that occur in the air inside it. What would happen to the pitch of the pipe if the temperature of the air increases? Explain!
17. An organ pipe that is covered at one end produces a certain note. If the cover is removed from the end what will happen to the pipe’s pitch? Explain!
18. The column of air inside a “slide whistle” can be adjusted by a movable piston to lengths of 5.0 cm to 27 cm. (a) The highest frequency note it plays is how many times greater than the lowest note? (Assume both notes are in the fundamental mode of resonance.). (b) Given that every octave is a doubling of frequency, how many octaves can it produce?
19. A kid has a straw in his soda. He blows across the end of the straw and produces a high-pitched sound. What would be the possible frequencies of sound produced if the open end of the straw is 7.00 cm above the level of the soda in the glass?
20. A certain bass guitar has a string that is 80.0 cm long that has a fundamental frequency of 55.0 Hz (the A string). (a) Determine the frequencies and wavelengths of the 2nd and 3rd harmonics for this string. (b) Determine the speed of waves traveling through this guitar string. (c) If another string on the same guitar is to have a fundamental frequency of 73.4 Hz, what must be the speed of waves in that string to produce this result?
21. I drive an old, kind of pathetic, cheap car. When I accelerate various things will rattle. For example the sun visors might start buzzing when I hit 30 mph. But then when I get to 35 mph the visors will stop buzzing and the glove box will start rattling. And then when I get to 40 mph the glove box stops rattling and some mysterious piece of loose metal somewhere hidden deep behind the dash will start humming. And so on. Explain what is going on here in terms of a source of vibration, standing waves, and resonance. (And be happy if your car doesn’t do this!)
22. Mr. M uses a microwave generator for classroom demonstrations. The generator produces microwaves at frequency of 10.525 GHz. In one demo the waves are reflected back toward the wave generator by a metal plate. As a microwave detector is moved through the region between the generator and the metal plate it is found that there are alternating regions of strong microwaves and no microwaves. (a) Describe what happens between the generator and the metal plate that produces the alternating pattern. (b) Determine the distance between one strong microwave reading and the next strong microwave reading.
23. In a popular do-it-yourself amateur scientist experiment a chocolate bar is placed in a microwave oven and zapped for about 30 seconds or so until melted “spots” form. Measuring the distance between melted spots and then multiplying by 2 and then multiplying by 2450 million Hz is “supposed to” yield the speed of light. The melted spots apparently get more energy (while in between it remains cool) – interference can explain this. (a) The hot spots are nodes or antinodes? Explain. (b) There is only one source generating microwave energy – if there is only one wave source explain some ways that it may be possible for interference to occur. (c) Explain why the procedure explained above should yield the speed of light.
24. The surface of a music compact disc has rows of “pits” that a laser reads when the CD is played. Such a disk is placed on the floor of a room and a laser is pointed straight down onto its surface. The rows of pits act like a grating (a “reflection grating”) and this produces an interference pattern on the 8.0 foot ceiling. There are a pair of bright spots 3.0 feet on either side of a point directly above the CD. (a) Determine the location of a second pair of dimmer spots on the ceiling. (b) Given that the rows of pits are separated by 1.5 μm what is the wavelength of the laser? (c) At what angles would antinodal lines appear if the experiment is repeated with a red laser of frequency 480 THz? (d) Essentially equivalent patterns could be produced with a transmission grating with how many lines per millimeter?
25. Light of wavelength 400 nm is incident on a pair of slits. An interference pattern occurs on a screen located 2.00 m from the slits. Bright fringes separated by 0.50 cm appear on the screen. (a) Determine the separation of the two slits. (b) A dark point on the screen between the 1st and 2nd order fringes is how much closer to one slit than the other? (c) What order line (in theory) should appear at an angle of 30.0° from the central line? (d) A single slit of what width in this same setup would replace the 1st order bright lines with dark lines? Explain.
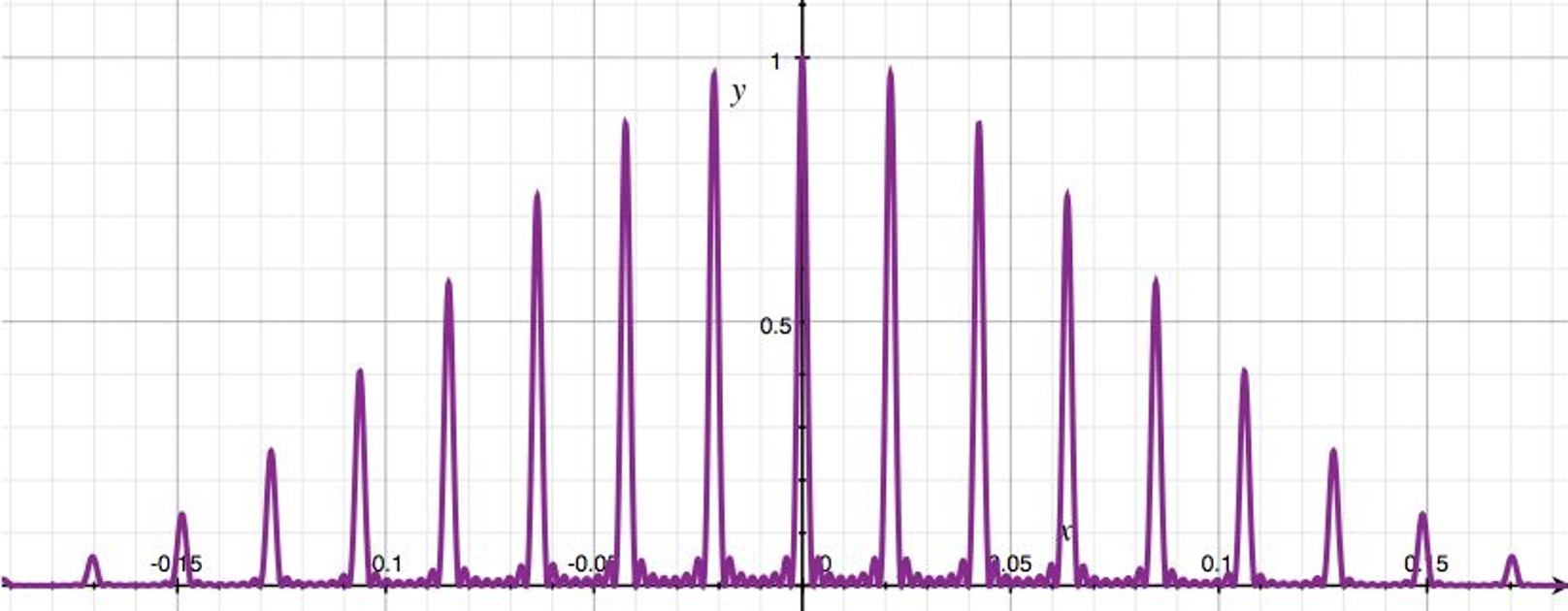
26. The following graph shows the
relative intensity of light versus angle for a two-slit interference pattern.
The angle value is in radians on this graph.
(a) At what angle (in degrees) is the 2nd order bright line? (b) At
what angle is there a nodal line along which the path difference is 2.5
wavelengths of the light? (c) How many times wider is the separation of the
slits than the wavelength of the light? (d) Sketch a graph of intensity versus
angle with all of the same parameters as this except it is produced by a
diffraction grating such that the light passes through many openings.
27. Laser light of wavelength 520.0 nm passes through two slits that are separated by 3.5 × 10-5 m. The light falls upon a screen that is 3.00 m away from the slits. (a) Determine the distance from the principle image to the 2nd order image. (b) Determine the distance between the dark lines that are observed on either side of the principle image.
28. Light of an unknown wavelength is passed through a diffraction grating with 460 lines/mm. The angle between the principle image and the 1st order image is 20.0°. (a) Determine the wavelength of the light. (b) Find the angle between the 1st and 2nd order images.
29. Monochromatic light of frequency 659 THz illuminates two slits separated by a distance of 1.79 μm. Find the angle between the antinodal lines of the first and second-order images.
30. A lecturer is demonstrating interference with sound waves. Two speakers are used, sitting 4.0 m apart on a stage in front of the room. The sound frequency is 325 Hz. Students sit in the front row of seats 4.5 m away from the stage. What is the spacing between the regions of destructive interference in the front row?
31. In a classroom demonstration
two speakers act in phase to produce sound with a frequency of 245 Hz.
Determine the type of interference that occurs for each of the following
students in the class: (a) Johnny is 2.00 m away from one speaker and 2.70 m
away from the other.
(b) Suzy is 0.50 m away from one speaker and 3.30 m away from the other. (c)
For each student give the path difference in multiples of the wavelength.