Standing Wave Lab

The purpose of this activity is to explore the properties of harmonics and standing waves.  Waves will be produced in an elastic cord using a mechanical oscillator driven by a sine function generator. 

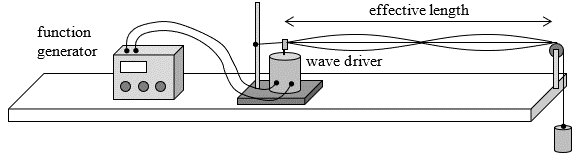
Procedure

1. Measure and record the mass of the elastic cord.  The same value appears in each data table.

2. Attach one end of the elastic cord to a ring stand.  Pass the other end over a pulley mounted at the end of the table and hang a calibrated mass of 100 g on the end of the cord.

3. Place the mechanical wave driver on the base of the ring stand with the cord passing through the “yoke” on top of the driver.  There should be very slight downward pressure on the yoke – but just enough to keep the cord in contact.

4. The effective length of the cord (in which there will be a standing wave) is measured from the yoke on the wave driver to the pulley.  The total length of the cord includes the entire cord – from the ring stand to the hanging mass.  The linear density (mass per length) of the cord is dependent on its total stretched length.

5. Use two jumper cables to connect the wave driver to the output of the sine wave generator. 

6. Set the amplitude at zero (all the way left), then turn on the generator.  Then gradually turn up the amplitude to about ¼ turn.  You should see the yoke moving up and down.  Do not turn the amplitude all the way up!  The wave driver only needs to be vibrating slightly.  Do not overdo it – knob should never go past half way!

7. Adjust the frequency until you observe harmonics in the cord.  Observe the frequency of several harmonics and determine the best value for the frequency of the fundamental.  (Note:  the “best value” for “fundamental frequency” is open to interpretation and you will be asked to explain what you do here – see question 1.)  Measure and record the effective length and fundamental frequency of the standing wave.

8. Change the effective length of the cord without changing the tension.  Simply move the ring stand and wave driver to adjust the distance from the pulley.  When you do this, tension and total length should remain the same, but the effective length of the standing wave is different.

9. Repeat the process to find the fundamental frequency at various effective lengths – use a range of values suitable for graphing – for example 0.2 m, 0.4 m, 0.6 m, 0.8 m, 1.0 m.  Note: measure and record the length as precisely as possible –  don’t waste time trying to “set the length” to some particular value!

10. Second set of data:  Change the tension in the elastic cord by doubling the mass hanging at the end.  Note that this will change the total length of the cord!  Therefore, you will need to measure and record the new total length of the elastic cord.

11. Complete the second table:  Determine the fundamental frequencies of harmonics, now at a different tension but a similar set of effective lengths as shown in the first data table.

Analyses

1. Calculate the weight of the calibrated mass that was hanging from the cord for each data table.  Recall that “weight” is equivalent to the amount of gravity acting on an object.

2. Complete the third column in the two tables by determining a quantity that can be used to create a linear graph showing the relationship between the harmonics formed and the effective length of the cord.  The slope of this graph can be used to determine the speed of waves in the cord.  (Note: there is more than one “correct answer” for the third column!)

3. Create a single graph based on the third column for both data sets.  Determine the line of best fit for each data set.  Show the results on the graph.  There should be a key or legend and unique colors and/or symbols to identify each data set.

Questions  (Write answers in complete sentences.)

1. Explain the method by which your group used multiple observed harmonics to determine the single value of fundamental frequency shown in each row of the data tables.

2. Using one or both of the coefficients of the lines of best fit, determine the speed of the waves in the cord for each data set.  Show your work!

3. (a) Calculate the theoretical speed of transverse waves in the cord for each data set based on the mass and total length.  (b) For each data set determine the percent difference between the theoretical speed and the speed determined using the line of best fit.  Show your work!

4. Discuss experimental error.  This should be a concise paragraph or two that describes signs of error apparent in the results shown in your report, and the most plausible sources of error that are responsible.

Completed Report:

· Completed data table

· Single graph with all data and two lines of best fit

· Answers to questions

Data

Calibrated mass on end of cord:		100.0 g
Weight of calibrated mass:
Mass of elastic cord:
Total length of stretched cord:
Effective Length (m)	Fundamental Frequency (Hz)

Calibrated mass on end of cord:		200.0 g
Weight of calibrated mass:
Mass of elastic cord:
Total length of stretched cord:
Effective Length (m)	Fundamental Frequency (Hz)