Physics 2 - Thermodynamics Assignment

AP Physics 2 Assignment – Thermodynamics

Reading Sections: 13.1 – 4; 14.1, 5; 15.1 – 6, Open Stax College Physics
Sections: 12.1 – 7; 15.1 – 7; 16.1 – 4, College Physics, Etkina et. al.

Objectives/HW

	The student will be able to:	HW:
1	Define and apply concepts of internal energy, thermal equilibrium, zeroth law of thermodynamics, and temperature.	1 – 3
2	State and apply the ideal gas law in terms of Boltzmann’s constant and solve related problems with variables pressure, volume, and temperature.	4 – 7
3	State and apply the stipulations of the kinetic theory of gases and solve related problems involving pressure, force, kinetic energy, Boltzmann’s constant, temperature, and speed distributions of particles	8 – 13
4	Define and apply the concept of thermal conductivity and solve related problems involving heat flow.	14 – 19
5	State and apply the first law of thermodynamics and solve related problems including work, heat, heat engines & cycles, P-V diagrams.	20 – 26
6	Define and describe entropy; state and apply qualitatively the second law of thermodynamics.	27 – 30

Homework Problems

1. A pot of water is on the stove. The temperature of the water increases until it starts to boil. (a) Describe how the motion of the molecules is changing as the temperature increases, before the water starts to boil. What type of energy is changing? (b) Once the boiling begins, the temperature stops increasing. Describe how the state of the molecules is changing as the water boils. What type of energy is changing?

2. A few drops of ice-cold water spills on a countertop. Over a period of time it may be observed to evaporate and “disappear”. (a) Determine the approximate change in temperature of the water and describe the mechanism(s) by which this occurs. (b) Explain how the water evaporates without boiling by discussing the concepts of internal energy of the water and random motion of the molecules.

3. A metal block has a narrow hole into which a thermometer is inserted and the temperature reaches 30.0 °C. The same thermometer is removed from the block and placed in a container of water and it settles on 10.0 °C. The thermometer remains in the water and the metal block is then submersed in the water. (a) Suppose the temperature of the water were to decrease after the metal block is submersed – would this violate the principle of conservation of energy? What would have to happen to the temperature of the metal block? (b) Explain why the temperature of the water would surely increase. (c) If the temperature of the water eventually settles at 13.0 °C what is the final temperature of the metal block? Explain how this conclusion relates to the zeroth law of thermodynamics.

4. Why is the air in the second floor of a house warmer than the air in the basement of the house? Explain by referring to gas laws, density, buoyancy, etc.

5. A particular vehicle’s tire has a volume of 12.0 L and is inflated with nitrogen (N₂) to a gauge pressure of 221 kPa (32.0 psi) on a day when the temperature is 25.0 °C. (a) Use the Boltzmann constant to determine the mass and number of nitrogen molecules in the tire. (b) The seasons change and the temperature is now 0.0 °C. Determine the new pressure reading of the tire by assuming the change in volume is negligible. (c) By what percent approximately does the area in contact with the roadway change with the different pressure? Why does this affect fuel economy? (d) How much nitrogen must be added to the tire to return it to the original pressure?

6. A metal cylinder is used to store compressed helium gas at a laboratory. A gauge on the cylinder initially reads 14.0 atm. After a certain amount of gas has been removed the gauge reads 12.0 atm. What percent of the helium stored in the cylinder has been used?

7. A bubble of methane with diameter 5.0 mm forms and escapes from the bottom of a lake where the temperature is 5.0 °C and depth is 60.0 m. Determine the approximate diameter of the bubble as it reaches the surface where the water temperature is 18.0 °C.

8. A vacuum is sometimes described as an “absence of matter”. Hmm. Let’s consider an “ultra high vacuum” (UHV) used for certain scientific equipment and experiments. Suppose such a system achieves an absolute pressure of 90.0 nPa at a temperature of 273 K. (a) Determine the number of molecules per cubic centimeter. (b) Compare this to the vacuum conditions of outer space, which has about 1 atom per cubic centimeter at 2.9 K – calculate the pressure. Is this UHV? (c) Find the root mean square speed of the atoms in space – mainly monatomic hydrogen (i.e. singular protons).

9. The “solar wind” is a steady flow of protons away from the Sun. (You can find the daily values of speed and density at spaceweather.com.) Some typical values: speed = 310 km/s, density = 3.0 protons/cm³. (a) Use these values to calculate the temperature and pressure based on the gas laws. (b) Explain why these values are not necessarily valid based on your understanding of the kinetic theory of gases. (c) What would it be like to stand in this wind? Would it burn you? Could you feel it blowing? Discuss and/or make some calculations…

10. Venus has a dense (65 kg/m³) atmosphere at high pressure (9.3 MPa) and temperature (730 K). (a) Determine the mass, kinetic energy, and average speed of the molecules in the atmosphere. (b) Show that these numbers are consistent with an atmosphere made almost entirely of carbon dioxide. (What percent?!) (c) What would be the force of buoyancy on a person of mass 81 kg in this atmosphere? (Venusian surface gravity: g = 8.87 N/m)

11. Derive an expression for the pressure P of a gas of density ρ with molecules that have a root mean square speed v_rms.

12. A common way to model the temperature change of a substance is to use an equation Q = mcΔT, where c is a constant called the specific heat (usually in units such as J/kg×K), and Q is heat – the transfer of thermal energy to the substance. (a) Derive an expression giving c for a monatomic gas in terms of the Boltzmann constant k, the atom’s mass m, and any appropriate constants. Assume the volume does not change. Hint: thermal energy for a monatomic gas comes only in the form of translational kinetic energy. (b) Find the value of c for helium in standard SI units. (c) Find the heat needed to increase the temperature of 70 grams of helium in a tank from 0.0 °C to 20.0 °C.

13. To help you understand “root mean square” consider the following set of eighteen atoms: four with speed 250 m/s, eight with speed 500 m/s, five with speed 750 m/s, and one with speed 1000 m/s. (a) Determine the mean speed. (b) Determine the root mean speed – the square root of the mean of the square of the speeds. (c) Sketch a rough graph of this speed distribution and show where the mean speed and the rms speed are located.

14. A certain sliding door has glass of thickness 3.0 mm and thermal conductivity 0.83 J/s×m×K, and dimensions 0.76 m by 1.8 m. (a) Find the rate of heat flow through the glass when the temperature difference of the air on either side is 2.0 C°. (b) The energy equivalent of a cookie (630 kJ, 150 cal) flows through the glass in how much time? (c) Suppose the glass breaks and it is replaced temporarily by a sheet of plywood with thickness 9.5 mm and conductivity 0.11 J/s×m×K – find the new rate of heat flow.

15. A beaker of water is boiling on a hot plate. Suppose that 50.0 grams boils away in 3.00 minutes. The latent heat of vaporization for water is 2260 J/g. The bottom of the beaker is pyrex glass with conductivity 1.2 J/s×m×K, area 75 cm², and thickness 0.10 cm. (a) What rate of heat flow is necessary to maintain the boiling described here? (b) Determine the temperature of the part of the hot plate that is in immediate contact with the glass.

16. Draw an analogy between thermal conductivity and electrical resistance. Electrical resistivity is a property of a material, but resistance is equal to the ratio of potential difference to rate of charge flow (i.e. current) for a particular object. Consider a new concept, thermal resistance, defined as the ratio of temperature difference to rate of heat flow for a particular object. (a) Derive an expression for thermal resistance R_t in terms of thermal conductivity k, cross sectional area A, length L, and any appropriate constants. (b) Would the rules for finding equivalent resistance for series or parallel resistors be valid with the quantity “thermal resistance”? Discuss and explain similarities and differences.

17. The ceiling of a certain room is 20.0 m² of sheetrock (k = 0.16 W/m×K) 13 mm thick covered by a layer of fiberglass insulation (k = 0.046 W/m×K) 3.0 cm thick. (a) Determine the heat rate through the ceiling to the air in the attic with a temperature difference 3.0 C°. (b) How much of the temperature difference occurs across just the sheetrock? Does it matter which side of the ceiling is hotter? Why or why not? (c) In order to cut the heat loss in half, how much fiberglass should be added?

18. A particular hot air balloon has volume 2840 m³ and carries a payload of 695 kg (basket, passengers, balloon material). Model the balloon as spherical. The thickness of the nylon material is 0.10 mm and has thermal conductivity 1.2 W/m×C°, Molar mass of air is 29.0 g/mol. (a) Estimate the power required to keep the balloon aloft in air at 20.0 °C using concepts of gas laws, buoyancy, and an assumption that heat loss occurs solely by conduction through the nylon. (b) A balloon like this has a burner system that may deliver heat at a rate of about 3 MW – explain any discrepancy.

19. Consider what is happening when you feel cold. (a) If you touch something and you get the sensation of coldness it may seem like the “cold is seeping into your bones” – of course that is untrue. Explain in terms of temperature, thermal equilibrium, and internal energy. (b) If you touch a metal wrench and then a block of wood, both at room temperature, the wrench feels colder – explain in terms of conduction. (c) If you step outside on a cold, crisp, clear winter evening you feel cold in spite of being surrounded by air, which has very low thermal conductivity (it is a very good thermal insulator) – explain.

20. A cylinder with a movable piston at one end contains an ideal gas. Describe events/actions that would increase the internal energy of the gas with each of the following stipulations. And give the scientific name for each type of process: (a) constant temperature, (b) constant pressure, (c) constant volume, (d) no heat.

21. A certain quantity of gas has an initial internal energy of 625 J. (a) In a certain process no work is done but the internal energy changes to 605 J – find the heat. (b) In a second process positive work 35 J is done on the gas adiabatically – find the internal energy after this. (c) Finally, the temperature remains constant as 45 J of heat flows into the gas – find the work done on or by the gas in this final process. (d) Make a sketch of pressure versus volume for the gas showing all three processes. How could this be made to happen experimentally?

22. A cylinder of gas holds an ideal monatomic gas with initial volume 20.0 cm³, pressure 1.00 atm, and temperature 20.0 °C. The cylinder and gas are heated to 60.0 °C, causing a piston in the cylinder to move, allowing the volume to increase. (a) Determine the initial internal energy of the gas. (b) Determine the change in internal energy. (c) Find the work done by the gas on the piston. (d) Determine the heat that must flow.

23. A syringe containing 3.00 cm³ of argon is submerged in ice water with the plunger above the water line and free to move. With the plunger locked in place the syringe is removed from the ice water and allowed to come to room temperature 22.0 °C. Finally the plunger is released and allowed to move (disregard friction). (a) Find the amount of heat for the argon as it warms to room temperature. (b) Find the maximum pressure of the argon. (c) Find the final volume of argon. (d) Estimate the work done by the argon by using an average pressure during its expansion. (e) Find the heat for the argon as the volume expands. (f) Sketch a pressure versus volume graph illustrating the events in this problem – considering the curve, are the estimates for the expansion too high or too low?

24. A quantity of ideal monatomic gas is initially at volume of 80.0 cm³, pressure 100.0 kPa, and temperature 300.0 K. The gas is compressed to a volume of 78.0 cm³ and pressure 104.3 kPa. (a) Determine the change in temperature. (b) Find the change in internal energy. (c) Determine the work done on the gas by assuming the P-V diagram is linear for this process. (d) Are the values in this problem consistent with an adiabatic process? Explain.

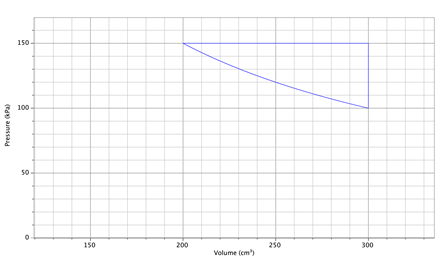
25. A heat engine employs three processes illustrated in the P-V diagram shown below. The working fluid is an ideal monatomic gas, which undergoes an isobaric expansion, an isochoric cool-down, and an isothermal compression at 300.0 K. (a) Use the values from the graph to find the number of atoms. (b) Find the greatest temperature attained by the gas – where on the graph does this occur? (c) Determine the work for the isobaric expansion. (d) Estimate the work during the isothermal process by area under the curve (or integrate if you know how!) (e) Determine the efficiency of the cycle.

26. A certain heat engine cycle starts at pressure P and volume V. In process 1 the pressure increases to 2P as volume stays constant at V. In process 2 the volume increases to 2V as pressure stays constant at 2P. In process 3 the pressure decreases to P as volume stays constant at 2V. Process 4 returns the monatomic ideal gas to its original state as pressure remains at value P. (a) Make a P-V diagram of the cycle. (b) Show that the internal energy of the gas ranges from ³/₂PV to 6PV over the course of the cycle. (c) Show that the net work done by the gas over the course of one cycle is PV. (d) Determine the efficiency of the cycle.

27. A warm cube of metal is placed into a cool cup of water that is at a lower temperature than the cube. (a) Explain why it would not be a violation of the first law of thermodynamics for the cube’s temperature to increase. (What would have to happen to the water)? (b) Explain why it would be a violation of the second law of thermodynamics if the cube’s temperature increases. (c) Would there be some atoms in the water that have more kinetic energy than some of the atoms in the cube? Explain.

28. A lump of clay is dropped onto the floor and stops moving. (a) Explain how the falling lump’s kinetic energy is transformed but nevertheless conserved. (b) Explain how this event relates to the second law of thermodynamics. Is there an increase in disorder? Is a lump of clay at rest on the floor “more orderly” than a falling and accelerating lump of clay? (c) Explain what would have to happen for the clay to spontaneously reverse its actions and how one could argue that this is not necessarily impossible but rather just extremely unlikely (to the extent that it is virtually impossible).

29. A cube of ice that melts is an example of increasing entropy as heat flows into it. But in order to form the cube in the first place heat had to be removed from water to decrease its temperature. (a) Does the entropy of the water in an ice cube increase as it forms? Explain. (b) What about the entropy of the environment around the ice cube as it is forming? For example, if the ice cube is formed in an electric freezer, what happens in the room at the same time it is freezing? By the second law of thermodynamics what must happen in the room (and how does it happen)?

30. The change in the entropy S of a system at a constant absolute temperature T is given by ΔS = Q/T, where Q is the heat flow into the system (negative if flowing out). As an illustration of this, consider the isothermal curve on the graph from problem 25 (and ignore the other parts of the cycle). (a) Calculate the change in entropy and determine which way would be an increase – left to right or right to left. (b) If the curve were extended in either direction how would this affect the amount of change in entropy? (c) Explain how this illustration correlates with the concept that naturally occurring processes lead to greater disorder and less availability of energy.

Selected Answers