AP Physics 2 Assignment – Optics
Reading Sections: 25.1
– 7; 27.7 Open Stax College Physics
Sections: 22.1 – 7; 23.1 – 8; 24.2, 24.4
Etkina et. al.
Objectives/HW
|
|
The student will be able to: |
HW: |
|
1 |
State and apply laws of reflection and refraction, Snell’s Law, and solve related problems and/or describe qualitatively the phenomena of absorption, transmission, dispersion, and reflection of light undergoing a change in medium. |
1 – 7 |
|
2 |
Solve problems involving thin film interference by relating wavelength, film thickness, and indices of refraction to path difference and type of interference. |
8 – 10 |
|
3 |
Apply the ray model of light to explain and analyze formation of real and virtual images by plane, concave, and convex mirrors and solve related problems involving object and image distance, magnification, focal length and/or radius of curvature. |
11 – 16 |
|
4 |
Apply the ray model of light to explain and analyze formation of real and virtual images by converging or diverging thin lenses and solve related problems involving object and image distance, magnification, and/or focal length. |
17 – 23 |
Homework Problems
1. A beam of light reflects off a mirror. The angle of incidence is 20.0°. (a) Determine the angle between the reflected beam and the incident beam. (b) Determine the angle between the reflected beam and the surface of the mirror (in the plane of the two beams).
2. Water has an index of refraction equal to 1.33. A laser with wavelength 405 nm is shone at an angle 30.0° relative to horizontal into a pool – some light goes into the water and some is reflected. (a) Find the speed and wavelength of light in the water. (b) Determine the angle of refraction. (c) Determine the angle between the transmitted beam of light and the reflected beam. (d) If the laser beam then enters a vertical piece of glass covering an underwater light, what index of refraction would cause it to change direction by 7.0°?
3. “Snell’s window” is an optical phenomenon that can be seen by a scuba diver looking at the surface of the water from below (search for images online!) The observer sees light from the sky and surroundings transmitted through an apparent circular “window”. Beyond the edge of this circle the only light visible is reflected light coming from below. Use an index of refraction 1.34 for saltwater. (a) Find the angle between a vertical line and a line of sight looking at the edge of this window. (b) The window would have a diameter of what value seen from a depth of 3.0 m? (c) The window is effectively a “fisheye lens” giving the diver a full “360-degree” (or 180 degree wide) view of everything above the surface – explain why.
4. Fiber optic cables transmit light by total internal reflection. Light exiting the end of the cable can deviate from the axis of transmission by an angle not exceeding that which satisfies the expression sin θ = (n2 – 1)½, where n is the index of refraction. Derive this formula or show why it works by using some example numbers. Hint: any light exiting the end must have undergone total internal reflection inside the cable.
5.
A beam of light
traveling parallel to one side of an equilateral triangular acrylic prism
travels through and exits along a path that is either parallel to its original
direction or bent downward as shown in the diagram. Suppose the acrylic has
index of refraction 1.49 and sides of length 6.00 cm.

(a) Determine the angle of refraction as the light enters. (b) Determine by
calculation whether or not total internal reflection occurs if the beam hits
the bottom surface of the prism. (c) If the beam exits in a parallel direction
what is the greatest distance that it could be offset (i.e. shifted
down) from the incident beam? (d) If the beam exits “bent” then what angle
does it deviate from the original (horizontal) direction?
6. Consider a beam that exits bent downward in the previous problem. If the incident light is white it is observed that the exiting beam will be a narrow rainbow of colors with red on the top and violet on the bottom. (a) Which color of light is traveling fastest through the prism? How do you know? (b) The index of refraction is very slightly different for the different wavelengths – does it increase or decrease with increasing wavelength? Explain. (c) Make a careful sketch of a single ray entering that splits into a red and a violet beam by the time it exits. Does the separation occur before it exits or only after it exits? Explain.
7. Although refraction and reflection are readily apparent with light, the same phenomena can occur with sound. (a) Starting with Snell’s Law, derive a formula relating the angles of incidence and refraction to the speeds in the two media (not the indices). (b) Given that sound has speed 343 m/s in air and 1500 m/s in water find the angle of refraction for sound entering water at an angle of incidence 10.0°. (c) Can sound undergo “total internal reflection” at a water/air boundary? Under what circumstances?
8. A soap bubble has air on both sides of thin layer of soapy water with thickness 366 nm and index of refraction equal to 1.33. Suppose light of wavelength 650 nm is incident on the thin soapy film with an angle near zero. (a) Determine the wavelength of the light traveling in the soapy water. (b) Determine the number of wavelengths of light equal to the thickness of the thin film. (c) Light that reflects off both surfaces (inside and outside of the bubble’s wall) would undergo constructive interference – explain why and support mathematically. (d) If the same thin film is lying atop a piece of glass there would be destructive interference with this same wavelength light – explain why.
9.
A thin film of
material with index of refraction 1.35 coats a glass lens with index of
refraction 1.52. The thin film is designed to eliminate reflections of light
with wavelength 550 nm. Assuming the incident and reflected light is nearly
normal to the surface, determine the thickness of the film.
10.
Two perfectly
flat panes of glass are stacked atop one another. Then a thin piece of foil of
thickness 2.50 × 10–6 m is placed between the two pieces along one
edge. This creates a wedge-shaped pocket of air in between the two panes.
Monochromatic light reflecting in a direction that is nearly normal to the flat
panes is seen to have 10 bright and dark fringes.
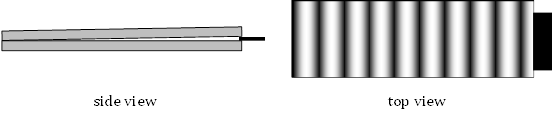
(a) The thickness of the “wedge of air” approaches zero at the left end of the
pattern – explain why this is a dark band of destructive interference. (b) The
center of the first bright band from the left corresponds to a thickness equal
to one fourth of the wavelength – explain why this is the case. (c) Given that
the “center” of the 10th bright band (greatest constructive
interference) occurs at the thickness of the foil determine the wavelength of
the light.
11. A typical concave “shaving mirror” has a focal length of 25.0 cm. (a) Assuming a spherical surface what is its radius? (b) If held 15.0 cm in front of your face what is the image distance and magnification? (c) Make a ray diagram of this mirror projecting an image of a nightlight onto an index card that is held 30.0 cm from the mirror and calculate the distance to the nightlight. (d) Determine the magnification of the nightlight image and describe it as real or virtual and inverted or erect.
12. A Newtonian telescope employs a parabolic mirror that focuses starlight and a secondary plane mirror that redirects the image out a hole in the side of the telescope tube. A certain such scope has the secondary mirror located 95.0 cm from the primary mirror, which has focal length 1200 mm. (a) How far from the secondary would images of stars form? A piece of film or digital detector can be placed here to record the image. (b) If the telescope is focused on a bird in a tree 50.0 m away how much does this move the image? In what direction?
13. A traditional headlamp in a car has a very bright filament that acts as a point source and a concave mirror that directs the light in front of the car. (a) If the filament is located exactly at the focal point of the mirror what would characterize the headlight beam of light? (b) If it is desired that the headlight beam spread out slightly, then where should the filament be located relative to the focal point (on which side of it)? (c) Make ray diagrams supporting each answer.
14. A convenience store uses convex mirrors to allow the cashier to watch for shoplifters. One such mirror has a radius of curvature of 12 inches. The 6.0 foot tall cashier can see a tiny image of himself 3.0 inches tall in the mirror. (a) Determine the focal length of the mirror. (b) Determine the distance from the mirror to the cashier and the position of the image relative to the center of the mirror’s spherical surface.
15. “Objects in mirror are closer than they appear” is a warning on the side mirror of a car. The mirror has a focal length of 0.50 m. Suppose you view a 4.3 m tall tractor trailer in the mirror and it is 10.0 m from the mirror. (a) Determine the image distance and height. (b) Discuss qualitatively what makes the truck appear farther away than it really is? How much closer is it than it appears do you think (don’t have to solve analytically)?
16. (a) Explain why it is not possible to project an image of an object onto a screen using only a convex mirror or a plane mirror. (b) Under what circumstances does a concave mirror produce a virtual image?
17. Suppose you find a magnifying glass in a junk drawer at home. You place it directly in between a light bulb and the wall, which are separated by 95 cm. When the lens is 15 cm from the wall it creates a focused image of the bulb. (a) Determine the focal length of the magnifying glass lens. (b) Without moving the light bulb (or the wall) at what other location would the lens project a focused image of the bulb on the wall? (c) Find the ratio of the image sizes of the two cases. (d) If the bulb is moved too close to the wall there will be no way possible to project a focused image – determine this distance and explain.
18. Suppose you wish to start a fire by igniting a piece of paper with a lens. (a) What type of lens must it be – converging or diverging, or would either type work? Explain. (b) How can you tell the type of lens by looking at the shape of the glass? (c) Explain why holding the paper at the focal length of the lens would give the best chance of ignition. (d) Even if the lens is perfectly shaped and has no flaws the light of the Sun will not be focused into an actual point, but rather the best you can do is to form a very small illuminated circle on the paper. Explain why.
19. The simplest camera design involves a lens focusing an image onto a piece of film or digital chip for the purpose of recording. Suppose the lens has focal length 50.0 mm and an object is located 4.00 m away. (a) Determine the distance from the lens to the film to obtain a proper focus. (b) If the subject moves closer to the camera to a distance of 2.00 m – find the required displacement of the lens relative to the film to maintain focus.
20. Consider the simple camera described above. A lens with a greater focal length is sometimes called a telephoto lens because it results in a magnified picture of a distant object. For distant objects the image forms essentially at the focal point of the lens. (a) Use this idea to derive an expression for the height of the image hi on the film in terms of the height of the object ho, its distance d from the camera, and the focal length f of the lens. (b) How does the expression show that greater focal length yields magnified images? e.g. Doubling the focal length has what effect on the size of the image on the film?
21. A person that is nearsighted cannot focus on objects that are too distant (hence their sight is limited to the nearby world). This can be corrected by wearing eyeglasses that are diverging lenses. A typical focal length would be 40.0 cm. Suppose a person wearing such eyeglasses looks at an object that is 18 cm tall and 1.10 m away. (a) Determine the image distance and height. (b) Make a careful ray diagram and explain how it shows that the lenses serve the purpose of “bringing the object closer” so the person can focus on it.
22. A one foot ruler is located 45 inches from a double concave lens, producing an image of the ruler 11 inches long. (a) Determine the focal length of the lens. (b) At what distance from the lens would the image of the ruler be 8.0 inches long? (c) When looking at the image of the ruler would the numbers on it appear upside down? backward? normal? Explain.
23. (a) Make careful ray diagrams showing every way possible a single lens of either type could produce an image of either type that has a magnification of ±½. Label the diagrams – object, image, type of lens, type of image, etc. (b) What if you reverse the labels “object” and “image” and the direction of the arrows – would the diagrams still be correct (i.e. a physically possible situation)? Explain.
Selected Answers