AP Physics 2 Assignment – Magnetism
Reading Sections: 22.1
– 11; 23.1 – 7, Open Stax College Physics
Sections: 20.1 – 14; 21.1 – 5, Giancoli
Objectives/HW
|
|
The student will be able to: |
HW: |
|
1 |
Define and illustrate the basic properties of magnetic fields and permanent magnets: field lines, north and south poles, magnetic compasses, Earth’s magnetic field. |
1 – 4 |
|
2 |
Solve problems relating magnetic force to the motion of a charged particle through a magnetic field, such as that found in a mass spectrometer. |
5 – 11 |
|
3 |
Solve problems involving forces on a current carrying wire in a magnetic field and torque on a current carrying loop of wire in a magnetic field. |
12 – 18 |
|
4 |
State and apply relation between magnetic field and position for a long current carrying wire and solve related problems. |
19 – 23 |
|
5 |
Qualitatively describe and apply properties of magnetic dipole fields generated by loops of current and model behavior of magnetic materials using domains, ferromagnetism, paramagnetism, and diamagnetism. |
24 – 29 |
|
6 |
State and apply Faraday’s Law and Lenz’s Law and solve problems involving induced emf and magnetic flux. |
30 – 37 |
Homework Problems
1. Scientists studying the Sun have determined that sunspots occur usually in pairs and are associated with the Sun’s magnetic field. The two spots in a pair can be distinguished magnetically as a “north” and a “south”. (a) If a compass were located in between two of the spots in a particular pair what direction would it point? (b) The magnetic field would point vertically upward from the surface of the Sun at which type of spot?
2. The needle of a compass is in fact a permanent magnet that generates its own magnetic field. Most compass needles feature a red end that points geographic north. (a) The red end of the needle is which magnetic pole of the needle? (b) The field generated by the needle tends to point in what direction relative to the Earth’s magnetic field?
3. A certain type of bar magnet is cylindrical and has diameter 1.20 cm. Centered along the sides the magnetic field parallels the cylinder’s axis and has strength 1.5 mT at a distance 1.20 cm from center and 1.10 mT at distance 2.4 cm from center. Suppose two such magnets are allowed to attract and stick to one another, side by side, north pole by south pole, and south pole by north pole. (a) Sketch the net magnetic field of the two magnets stuck together. (b) Use superposition to predict the strength of the net magnetic field 1.80 cm on either side of the shared line of contact. (c) How would the field of one magnet affect the field that exists along the centerline of the other magnet?
4. A ceramic disk magnet can be shaped about the same size as a quarter. Let’s call one side “heads” and the other side “tails”. Suppose the disk is placed in a strong magnetic field that is pointing vertically upward in a classroom and the disk is observed to “flip” so that “heads” is up. (a) What direction is the field of the disk magnet pointing once it is “heads up”? (b) The poles of the disk magnet are quite close to one another, but which one is closest to the “heads” side?
5. The Sun produces a “solar wind” that consists of charged particles such as protons and electrons streaming outward into space. Suppose the “wind” reaching the Earth has speed 500 km/s. These particles encounter the Earth’s magnetic field which has value 0.50 G pointing north near the equator. Consider what happens in this wind on the side of the Earth directly facing the Sun. (a) Determine the magnetic force acting on a proton and its resulting acceleration. (b) Repeat for an electron.
6. The Earth’s magnetic field in Knoxville does not point parallel to the ground. Rather it has components 22 μT northward and 45 μT vertically downward. (a) Determine the net magnetic field in this location and its direction relative to vertical. Now suppose a pith ball of charge –2.5 nC and mass 0.10 grams is dropped from a height of 1.5 m above the floor. (b) Determine the maximum magnetic force that acts on the pith ball as it falls. (c) Calculate the angle by which the acceleration of the pith ball varies from vertical at the instant it hits the floor.
7. Use the field described in the previous problem. A certain glass rod has mass 50.0 g and is given a charge +350 nC. (a) If the rod is launched with speed 45 m/s what is the greatest magnetic force that can act on it and what direction(s) should it be launched? (b) At the same speed what charge on the rod would be needed for the rod to experience a force with magnitude equal to its weight? (c) Using the given charge what speed would be needed?
8. A charged particle moving freely through a magnetic field will be accelerated by the field but its speed cannot be altered. (a) Explain why this is so. (b) Can a magnetic field do work (positive or negative) on a charged particle? Explain.
9. An alpha particle, mass 4.0 u and charge +2e is moving through a uniform magnetic field in a laboratory experiment. The field is 0.100 T vertically upward in the lab and the alpha particle moves in a circular path with radius 5.0 cm. (a) Determine the speed of the particle and direction or motion as seen from above. (b) Determine the frequency. (c) A singular proton moving at the same speed would have what radius circle? (d) In order for an electron to move identically to the alpha particle would require what magnetic field?
10. A particular mass spectrometer has a uniform magnetic field of 0.600 T and is designed to analyze charged particles moving at speed 2.6 × 105 m/s. (a) In order to “select” charged particles with this speed an electric field produces a force equal and opposite to the magnetic force – determine the required electric field. (b) Suppose singly and doubly ionized sodium ions (mass = 23.0 u) pass through the velocity selector and enter the region where only the magnetic field exists – determine the radii of the paths followed. (c) Now suppose singly ionized chloride ions pass through the same setup and are found to follow paths of radii 15.8 cm and 16.7 cm – determine the mass of the two isotopes in atomic mass units.
11.
A spectrometer
with the same design as that described in the previous problem has magnetic field
strength B and electric field strength E. (a) Derive an
expression for the mass m of a particle in terms of its observed radius r
and charge q. (b) In order for the velocity selector to function there
must be an electric field of a certain value existing between two oppositely
charged plates separated by distance d. Derive an expression for the
required voltage source V needed to charge the plates in terms of m,
r, B, d, and q.
12. A certain adjustable gap magnet has a very strong magnetic field of 0.60 T concentrated in a cylindrical space between two opposite magnetic poles of two magnets. A wire carrying a current of 3.00 A passes through the gap along its 2.0 cm diameter. (a) Supposing the south pole is on your left and the north pole is on your right and the current is away from you – determine the magnetic force on the wire. Ignore the weak field that exists outside the gap. (b) In order to increase this force to 1.0 N how much current would be required?
13.
Examine the
figure below that shows a battery and wire circuit. The wire in the circuit
forms a 30-60-90° triangle with hypotenuse of length 10.0 cm. The battery is
6.00 V and internal resistance 1.30 Ω. The entire circuit is immersed in
a uniform magnetic field 8.0 mT into the page. (a) Determine the force on the
hypotenuse. (b) Determine the force on the short side of the triangle. (c)
The net force for the entire triangle can be shown to be zero – would the same
be true of any dimension triangle? any shape circuit? Explain. (d) If the
wire is flexible it would tend to bend and take on what eventual shape? (e)
Would the force on the longest leg of the triangle be affected by the presence
of the battery? Explain.

14.
A rectangular
loop of wire has width 1.0 cm and length 6.0 cm and 50.0 turns. One of the
short sides of the loop is placed between the gap of a horseshoe magnet and it
is observed that the net force on the loop is at most 0.18 N out of the page when
it carries current 3.5 A. (a) Estimate the strength of the magnetic field in
the gap of the horseshoe magnet assuming it is negligible elsewhere. (b)
Complete the diagram shown below by showing the direction of the current and a
sketching the magnetic field. (c) The actual strength of the magnetic field in
the gap between the poles would be greater or less than calculated? Explain.

15.
Consider the
diagram shown below that shows a bar magnet and a circular loop of wire with
diameter 1.2 cm and current 0.50 A. Where the loop is depicted the field of
the magnet has magnitude 9.0 mT and forms an angle of 30.0° with the sides of
the magnet. (a) Determine the net force on the loop. (b) Describe
specifically changes in magnitude and direction of this force should the loop
move to other locations along the axis of the magnet. (c) Suppose the current
is reversed – does the bar magnet “repel” or “attract” the loop? Explain. (d)
If the loop of current behaves like a second magnet, being either attracted or
repelled by the bar magnet, where are the loop’s poles and what does its field
look like? Sketch!

16. A rectangular loop of wire carries a counterclockwise current of 0.83 A. The rectangle is 3.0 cm by 7.0 cm and consists of 75 turns. The loop is placed in a uniform magnetic field of 15 mT that parallels the long sides of the rectangle. (a) Find the amount of force on each side of the rectangular loop and explain why the net force on it is zero. (b) Determine the torque on the loop about an axis that is parallel to the short sides of the rectangle and show that the result is the same no matter where this axis is located. (c) Repeat both parts but with field parallel to short sides and axis parallel to long sides.
17. The basic principle of electric motors is torque similar to that found in the previous problem. It is possible to show that the maximum torque on a coil of wire is τ = NIAB, where N = number of turns, I = current, A = area bound by the coil, B = magnetic field assumed uniform. Show the steps to derive this expression by assuming a rectangular coil of height h and width w. Then repeat the steps from the previous problem.
18. Suppose it is desired to produce an electric motor capable of delivering a certain amount of torque τ using a certain voltage V. Inside the motor is a circular coil of radius R made of wires with resistivity ρ and radius r. (a) Derive an expression for the required strength of magnetic field B in terms of τ, V, ρ, r, and R. (b) Calculate the magnetic field given torque 80.0 Nm, voltage 18 V, resistivity of copper 1.68 × 10−8 Ωm, wire radius 0.32 mm, and coil radius 2.0 cm. (c) Does this seem practical? Discuss.
19. A long wire carries a current 5.00 A straight upward from floor to ceiling. (a) Determine the magnetic field produced at a location 1.00 cm north of the wire’s center. (b) Determine a location where this current creates a field equal to 0.50 G south. (c) Given that 0.50 G is the strength of Earth’s magnetic field what happens at that location? Discuss. (d) What current in the wire would produce a field equal to 1.0 T at a distance of 1.00 mm from center?
20. (a) Determine the maximum amount of force that a straight wire with current 2.00 A can exert on an electron with speed 1.5 Mm/s that passes within 0.50 cm of the wires center. (b) This force would be directly away from the wire if electron is moving in what direction? (c) Determine the radius of curvature of the electron’s path. (d) Sketch the electron’s path relative to the current if it is free to move unimpeded by any other forces.
21. A certain 10.0 m long extension cord has two parallel wires separated by 2.50 mm from center to center carrying current in opposite directions. The cord is used to power a 1.50 kW heater running on 120 V. Ignore variation in current that would exist for AC power. (a) Determine the net magnetic field strength at a point midway between the two wires. (b) There are certain locations where the magnetic field of one wire is twice the strength of the other – determine the two possible net magnetic fields at these locations. (c) Determine the total force of one wire acting on the other and describe as attraction or repulsion.
22. Time for a physics treasure hunt! Where is the proton? A current of 3.00 A flows in the positive direction along the x-axis of a coordinate system. A current of 2.00 A flows in the positive direction along the y-axis of the same system. The wires carrying these currents cross at the origin but insulation around the wires keeps the current separate. Somewhere in quadrant I or II of the x-y plane there is a proton that has velocity 1.4 × 107 m/s 45° and it is accelerating 1.4 × 107 m/s2 directly toward the origin. Where is it?!
23. A solenoid is a cylindrical coil of wire (looking a little like a spring or slinky) in which current spirals from one end to the other and sometimes back again. This arrangement generates a fairly uniform magnetic field inside the cylinder with strength approximated by B = μ0NI/L, where N is the number of turns, I is current, and L is the length of the cylinder. Using the wire that stretched from floor to ceiling from the previous problem it would be possible to form a solenoid of radius 1.0 cm with 48 turns and length of 5.0 to 10.0 cm. (a) Determine the magnetic field at these two possible lengths with the same 5.00 A current as before. (b) How many times greater are these fields compared to the previous problem? Explain the logic in this based on the superposition principle. (c) Why does the field depend on the length when number of turns and current are the same?
24. Suppose you are holding a bar magnet looking directly at the north pole (the south pole is on the opposite side from your view point). (a) The majority of domains in the magnet must have which pole facing you? (b) Explain why it is not necessary that all of the domains face one way. (c) The charges within the majority of domains are circulating or “spinning” in which direction from your perspective – clockwise or counterclockwise? (d) If the magnet is heated to a high enough temperature it may lose its strength – explain what happens to the domains.
25. The iron in an ordinary nail has domains that are randomly oriented. Suppose a bar magnet is brought near the nail and the head of the nail is attracted to and sticks to the north pole of the magnet. (a) The fields of the domains that were randomly oriented now are tilted to point mainly in what direction – toward the head of the nail or opposite? (b) Imagining each domain to have a north and south pole, how does this help explain the attraction to the magnet? (c) How is the situation different if the head of the nail sticks to the south pole of the bar magnet?
26. A ferromagnetic rod or a paramagnetic rod will tend to align with an external field such that the field aligns with the long axis of the rod – why? To answer this question sketch a rod parallel to an external magnetic field and sketch another rod perpendicular to an external field. Then add arrows inside the rod representing dipoles within domains or atoms. Recalling that each dipole acts like a little magnet itself, consider how the tiny dipoles within each rod interact with one another. Now explain why the rod aligns parallel to the field!
27. A diamagnetic has dipoles that tend to align opposite to an external field. Repeat the above exercise but this time explain why this type of rod would align perpendicular to an external field.
28. An electromagnet is formed by placing a ferromagnetic material inside a solenoid coil. A particular such magnet has a coil with 250 turns, length 12 cm, current 0.40 A, and is wrapped around a steel bolt. The resulting magnetic field is 35 mT. (a) By what factor does the steel increase the magnetic field produced by the coil? Explain what is happening inside the steel for this to happen. (b) What is the strength of the field produced by the steel?
29. In electrostatics it is observed that a neutral object can be attracted to either a negative or a positively charged second object because of induction. Discuss the similarities with ferromagnetic or paramagnetic materials in the presence of a permanent magnet.
30. A bar magnet is dropped through a vertical copper pipe. The north pole of the magnet is facing down as it falls. Describe answers as viewed from directly above the pipe. (a) In what direction is the induced current in the copper below the falling magnet? (b) In what direction is the induced current above the falling magnet? (c) Explain why this slows the falling of the magnet by making a sketch and labelling three sets of poles – those of the magnet and those of the two currents above and below it.
31. Suppose you have a bar magnet and a gold wedding band. (a) Describe at least two ways you can move the ring near the stationary magnet that would induce a current. (b) Describe at least one way the ring can be in motion near the magnet and have zero induced current.
32.
A wire is bent
into the shape of an equilateral triangle with sides of length 25 cm. The
triangle is placed in a uniform magnetic field as shown and the field varies
according to the following graph, changing from 0 to 0.8 T out of the page in 3.0
millisecond and then decreasing and reversing direction.
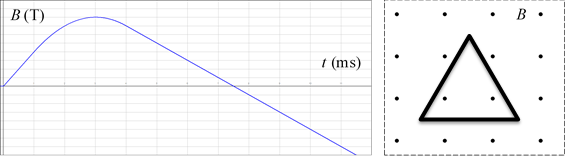
Determine the magnetic flux and the emf at: (a) t = 0.5 ms. (b) t
= 3.0 ms. (c) t = 6.5 ms, (d) t = 7.5 ms. (e) Sketch a graph of
the induced emf versus time.
33. A circular coil of wire with 300 turns and a radius of 10.0 cm is located in the Earth’s magnetic field, which has strength 0.50 G. Initially the coil is oriented so that the field is parallel to the diameter of the coil. The coil is then rotated so that the diameter is perpendicular to the field. (a) Determine initial and final magnetic flux for each single turn of the coil. (b) If the coil is reoriented in 0.10 s what is the average emf induced? (c) In order for the reorientation to produce 6.0 V, the reorientation must be done in how much time?
34.
A partial
circuit is formed by wires and a resistor of 33 Ω as shown. The circuit
is located in a uniform magnetic field of 0.20 T. A conducting bar completes
the circuit and is moved across the wires at a constant velocity 6.0 m/s, right.
(a) Determine the induced emf. (b) Find the current in the circuit and
describe its direction. (c) Determine how much force is required to move the
bar disregarding any friction. (d) Suppose the 25 g bar is at rest and the
resistor is replaced by a battery with emf 1.5 V and internal resistance 1.2
Ω. Find its initial acceleration and its eventual “terminal velocity” (given
sufficient distance to move).
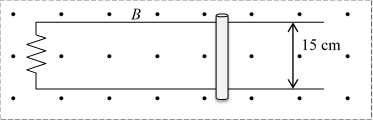
35. The antenna of a certain old car is simply a metal rod 0.30 m long sticking straight up from the fender. Suppose it is not connected to the radio and the car is traveling at 30.0 m/s west in an area where Earth’s magnetic field is horizontal and north with magnitude 48 μT. (a) Determine the magnetic force on a single electron in the rod. (b) Charge shifts inside the rod until there is an electric field that prevents further currents – determine the magnitude and direction of this field. (c) Given the field determine the potential difference of the top of the antenna relative to the bottom of the antenna.
36.
The square loop
of sides length s and mass m shown below is made of a single turn
of wire with radius r and resistivity ρ. Starting from rest
and adjacent to the field, the loop accelerates at constant rate a
directly into the uniform magnetic field B oriented as shown; the field
outside the dashed lines is zero. (a) Derive an expression for the maximum
current induced in the square as it enters the field. (b) Determine the force
that must act on the square at the instant just before it is fully inside the
field’s region. (c) Suppose that as soon as the square is completely inside the
field no forces act and it coasts at constant velocity to the other side.
Explain specifically what happens when the loop encounters the other end of the
field if no other forces act.

37.
An AC
transformer employs two coils of wire that share very nearly the same magnetic flux
at all times, but which are not connected electrically. When flux changes in
one coil it changes equally in the other (ideally). A certain transformer
takes 120 V AC and converts it into 6.0 V AC that is then converted to DC for
the purpose of charging a cell phone battery. The 120 V from the wall outlet
connects across the primary coil, which has 320 turns. This induces an emf of
6.0 V and current of 330 mA in the secondary coil which serves to charge the
battery. (a) Use Faraday’s Law to determine the rate of change in the magnetic
flux that exists in each turn for each coil. (b) Determine the number of coils that must be
present in the secondary coil. (c) Assuming 100 % efficiency (power output of
the transformer versus power input) determine the current in the primary coil.
(d) Derive expressions that relate the ratio of the number of turns in the
coils, NP/NS, to the voltages VP/VS
and currents IP/IS. (e) Explain how and
why a real transformer would differ from the ideal described here.
Selected Answers