AP Physics 2 – Electrostatics Review Problems
1. A hollow metallic sphere is given a net electrical charge. This charge will spread evenly across the surface of the sphere. (a) Use Coulomb’s Law to explain why any charge added to the sphere will go to the surface and spread out evenly. (b) A point charge is placed inside the metallic sphere. Although it may not be obvious to you, this point charge would not be attracted to or repelled by the charged surface of the sphere, even if it is not at the center of the sphere. Use Coulomb’s Law to explain how this is possible.
2. Two charged particles “floating in space” repel one another. One particle is a small piece of ice, which remains essentially at rest. The other particle is a speck of dust which moves directly away from the ice. At a separation distance of 0.40 m the dust speck has acceleration 6.0 m/s2 and speed zero. (a) Using only the given information, what specifically can you determine about the charges on the two particles? (equal? opposite? unequal? signs?) (b) What explanation is there for the ice having very little motion? (c) At what distance would the acceleration of the speck of dust be 3.0 m/s2? (d) Is there enough information to determine or estimate the speed at this point? Explain and/or solve.
3. Astronaut Steve, mass 95 kg, is headed out the door of his space capsule for a space walk and steps out into space, not realizing he forgot to attach himself to his tether! But wait – just as he stepped he scuffed his CPVC space boots on the woolen door mat and attained a net charge of –190 nC. Will he float away into space and perish?! Or will the principles of electrostatics save him?! Stay calm and read on. (a) By what principle can the net charge of the space capsule be determined? What charge would it have and where would it reside? (b) Find the force of attraction on the astronaut and the resulting acceleration when he has drifted to a distance of 5.00 m from the door mat. (c) Find the potential at this same point. (d) If he is moving away from the capsule at 1.1 mm/s at that same point, determine the potential difference through which he must drift before coming to a stop. (e) Determine the distance from the mat at which he stops, and his acceleration at that point. (f) Is he doomed?
4. Pick any two protons currently located anywhere in the universe – determine how many times greater is the electrostatic repulsion of these particles than the gravitational attraction of these two particles. Why does this not depend on separation distance of the two protons?
5. A pith ball of mass 0.20 grams is 0.50 m above a sphere with charge –3.5 μC. At this instant the pith ball is not accelerating but has velocity 2.0 m/s upward. (a) Determine the charge on the pith ball. (b) Determine the acceleration of the pith ball when it is 0.60 m above the sphere. (c) Determine the speed of the pith ball at this point – to get the exact value use potential difference and conservation of energy; to get a very good approximation use force, kinematics, and mean acceleration. It’s good practice both ways!
6. Consider what happens when an electric field causes the phenomenon called induction. Suppose a solid neutral metallic sphere of diameter d is held stationary inside a uniform electric field E that points upward. (a) Explain specifically how this affects charge within the neutral sphere. (b) Would there be a net force on the neutral sphere in such a scenario? If so, what direction? If not, why not? Explain. (c) Model the behavior as if inside the neutral sphere there are now two point charges separated by an amount half the diameter of the sphere. Derive an expression for the induced charge amount in terms of E, d, and appropriate constants. (Hint: forces become balanced – use Coulomb’s Law!) (d) Calculate this charge amount for E = 100 kN/C and d = 1 cm. (e) Does the result seem reasonable? What are problems with this model?
7. Three point charges, each +6.0 nC, are located at different corners of a square of sides length 70.0 cm. (a) Determine the electric field at the “empty” corner. (b) Determine the electric potential at the “empty” corner. (c) Repeat with two charges +6.0nC adjacent on one side and the third charge –6.0 nC at one of the remaining corners.
8.
At a distance d to the
right of a certain charge q1 there is an electric
field E pointing to the right. However, when an additional charge q2
is located at a distance d to the left of the first point charge, the
field in this same location as before now has the same magnitude E but points
to the left! This is shown in the “before and after” diagrams below. (a) What
are the signs of the two point charges and how can you tell? (b) Which charge
must have a greater absolute value and how can you tell? (c) Determine the
ratio of q2 to q1. (d) Make a careful
sketch of the electric field illustrating how the field of q2
“overpowers” the field of q1 as illustrated by the facts in
this problem.

9. A scientist performing Millikan’s experiment observes an oil drop that weighs 4.3 × 10–14 N levitating at rest between the two metal plates held at a potential difference 425 volts. The two horizontal parallel plates are separated by a vertical distance of 8.0 mm. (a) Determine the difference in the number of protons and the number of electrons in the oil drop. (b) What additional information would be needed to determine the sign of the charge on the drop? (c) If the voltage across the two plates is reversed what is the initial acceleration of the oil drop?
10.
Suppose there exists a region in
space with a uniform electric field 88 kN/C, 0.0°. A charged particle of mass
2.2 grams and charge –11 nC moves in this field with velocity 3.3 m/s, 60.0° at
time t = 0. (a) At a certain subsequent point the direction of the
velocity will be 90.0° – determine the speed and time at which this occurs.
(b) Through what potential difference has the particle moved to reach this
point? (c) At an even later point in time the particle returns to the same
equipotential line (isoline) on which it was located at t = 0. Where is
it then, and what is its speed?
Answers
1.
a. Electrons repel one another and
because the metal is a conductor the result is that electrons spread out evenly
across the surface.
b. At the center of the sphere the point charge is attracted or repelled in all
directions equally because the charged surface is in all directions at an equal
distance away. But if it moves, say to the left of center, by Coulomb’s Law it
is now closer to some charge on the left side of the sphere but there is more
charge located to the right of it that is farther away. It is possible (and in
fact it is the case) that the amount less that the charge to the right of it
acts because it is farther away is counteracted by the fact that there is a
greater amount of charge to the right than to the left of the point charge.
2.
a. Because the two particles repel
the sign of each charge must be the same – either both positive or both
negative. However there is no way to determine the relative amounts of charge
– the observed forces of repulsion are equal and opposite whether or not the
charge amounts are equal.
b. Because force is equal and opposite, the ice must have a much greater mass
than the speck of dust and therefore accelerate much less – a negligible amount
if the mass discrepancy is great enough (which must be the case by the
statements given).
c. 0.57 m
d. It might seem as if there is not enough information because mass and charge
amounts are unknown. However the speed at this point must be 1.2 m/s. This
can be estimated using kinematics, or it can be derived using conservation of
energy and potential difference.
3.
a. By conservation of charge the
net charge produced by the push off of the mat should be zero and therefore the
mat attains a net charge of +190 nC. Because wool is an insulator this
positive charge would be “trapped” there and “stuck in place” on the door mat.
b. attraction = 13 μN, acceleration = 1.4 × 10–7 m/s2
toward capsule.
c. 340 V
d. 300 V
e. 43 m, acceleration = 1.8 × 10–9 m/s2 toward capsule.
f. Well… he should eventually be returned to the capsule by this
electrostatic attraction, but it will take a long while. He better try to
conserve his oxygen…
4. The repulsion is 1.3 × 1036 times greater than attraction at any distance because both forces vary with the same inverse square relationship to separation distance.
5.
a. –16 nC
b. 3.0 m/s2 downward
c. 1.9 m/s (using ΔV = 10500 volts or using mean acc = 1.50 m/s2
downward)
6.
a. Being located in a conductor
the electrons within the sphere are free to move. The upward electric field
causes a downward force on the negatively charged electrons. However, once electrons
have moved toward the bottom of the sphere the top of the sphere is positive
due to the loss of electrons from atoms on that side. Hence, the top half of
the sphere is positively charged and the bottom half of the sphere is
negatively charged.
b. The net force on the sphere will be zero if the field is truly uniform.
This is because the force on every positively charged particle within the
sphere is balanced by the equal and opposite force on every negatively charged
particle within the sphere. If the sphere is neutral the number of protons
equals the number of electrons, which means the total force up equals the total
force down. The absence of a net external force means the sphere as a whole has
no acceleration or change in momentum due to the field. Any internal forces
between particles within the sphere are equal and opposite by Newton’s 3rd
Law and have no net effect on the motion of the sphere as a whole.
c. q = πε0Ed2
d. 0.3 nC
e. This is “in the ball park” of a typical charge found on a pith ball of that
size interacting with a Van de Graaff generator that produces a field of that
magnitude. However, the model is clearly too simple. In order for there to be
true point charges within the sphere electrons would need to converge on a
single point within the metal and the mutual repulsion guarantees this will not
happen. Instead the electrons will spread out on the surface of the bottom
half of the sphere, with greater density at the bottom. (In reality, there
would be no net charge anywhere inside the volume of the solid sphere and the
net electric field at all points in the metal would be zero.)
7.
a. 210 N/C away from center of
square
b. 210 V
c. 170 N/C tilted 64° outward from the negative charge , 55 V
8.
a. Charge 1 is positive because
the original field points away from it. Charge 2 must be negative in order to
cause the net field to reverse directions.
b. Charge 2 must be greater in absolute value because it is twice as far away
from the point in question and yet has a greater influence.
c. q2/q1 = –8
d. 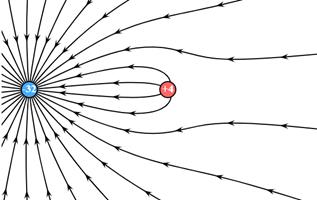
9.
a. 5
b. If the polarity of the plates is known the sign can be determined. For
example if the bottom plate is positive and the top plate is negative then the
charge on the oil drop is positive and it has lost 5 electrons.
c. 20 m/s2 downward (2g downward)
10. a. v = 2.9 m/s, at t = 3.8 s
b. –270 kV
c. v = 3.3 m/s at r = 21 m, 90° from its initial position.