AP Physics 2 Assignment – Circuits and Capacitors
Reading Sections: 19.5
– 7; 20.1 – 5; 21.1 – 6, Open Stax College Physics
Sections: 18.5 – 7; 19.1 – 10, Etkina et. al.
Objectives/HW
|
|
The student will be able to: |
HW: |
|
1 |
Define electric current and the ampere and solve problems relating current to charge and time and to power and voltage. |
1 – 3 |
|
2 |
Define resistance, resistivity, and the ohm and Ohm’s Law and solve related problems. |
4 – 10 |
|
3 |
Determine resistance for series or parallel combinations of resistors, state and apply Kirchoff’s node and loop rules and solve related problems, including analysis circuits with multiple batteries, resistors, and switches. |
11 – 15 |
|
4 |
Define and apply the concepts of internal resistance and emf to solve related problems with the standard model of the terminal voltage of voltaic cells. |
16 – 21 |
|
5 |
Define capacitance and relate to charge, voltage, energy, and time constant to solve related problems involving capacitors in circuits at steady states of charge or discharge and qualitatively describe transitions of such states. |
22 – 31 |
|
6 |
State the relation between capacitance, area, separation, and dielectric constant for parallel plate capacitors and solve related problems. |
32 – 37 |
Homework Problems
1. A particular cell phone has a rechargeable battery rated at 3.7 V and 1200 mAh. While in suspend mode the phone uses 75 mW power and while active it uses 650 mW (on average). (a) What is the total amount of charge that can pass through the battery before it dies? (b) Determine the current through the battery while in suspend mode. (c) If the phone is active only 5.0% of the time what is the total number of hours a full charge will typically last?
2. A driver leaves his car in the parking lot with the headlights on (and nothing else in the car draws significant current). Each headlight bulb has power 54 W and connects to the 12 volt battery. (a) How much charge passes through each bulb in 5.0 minutes? (b) What current must pass through the battery of the car and by what conservation law(s) can this be logically deduced? (c) The lead acid battery in a car involves a chemical reaction in which 2 electrons are liberated for every 1 lead atom that reacts to form lead(II) sulfate. In how much time do a trillion of these reactions occur if the headlights remain on?
3. A certain type of dimmer switch causes current to flow only for small periods of time. One possible setting would have the current to a 60 W light bulb flowing only one sixth of the time, causing it to appear dim. During every one second of operation there would be 120 “bursts” of current in alternating directions with each burst lasting 1.39 ms. (a) If each burst moves 0.246 mC through the bulb what is the average current of each burst? (b) What is the overall average current (realizing that for part of the time there is no movement of charge)? (c) During a single burst the current decreases very nearly linearly with respect to time – use this information to determine the maximum instantaneous current.
4. A battery rated 6.0 V is connected to a resistor rated 330 Ω. (a) Determine the current. (b) Determine the power. (c) Determine heat dissipated by the resistor in 1.0 hour.
5. The tiny incandescent bulbs in a string of holiday lights each have resistance 14 Ω while in operation and emit heat and light at a rate of 0.41 W. Determine the voltage and current requirements for such a bulb.
6. An electric stove eye operates on 240 V and heats 2 quarts of water to the boiling point in 8.0 minutes. Given that it takes 634 kJ of heat to increase the temperature of the water from 20 to 100 °C, estimate the current and resistance of the stove eye element. For each value state whether it is a “maximum possible” or “minimum possible” based on assumptions that are made.
7. Hey – are you holding a pencil right now? A typical #2 pencil has a graphite lead with radius 1.0 mm. In a particular experiment with such a pencil it is found that lead with length 15 cm has resistance 19.6 Ω. (a) If the pencil is sharpened and the length reduced to 12 cm what is the resistance of the lead? (b) If a pencil is made with the same materials but the radius is increased to 1.5 mm what is the resistance of lead with length 12 cm? (c) Determine the resistivity of the pencil lead. You might hear it said that the lead is graphite – does this numerical result support that? Look it up!
8. A typical circuit in your house might have 16 gauge copper wires of diameter 1.29 mm. Suppose such a wire inside the walls stretches a length of 5.0 m and carries a current of 12.0 amperes. (a) Determine the resistance of the wire given the resistivity of copper is 1.68 × 10−8 Ωm. (b) At what rate does the wire give off heat? (c) If replaced with 10 gauge wire, which has twice the diameter, what would happen to the heat given off for same current?
9. Two aluminum wires, ρ = 2.65 × 10−8 Ωm, each of length 40.0 cm and diameter 0.645 mm are used to connect a resistor of 5.00 Ω to a voltage source of 9.00 V. (a) Find the total resistance of the wires and resistor combined. (b) Determine the voltage drop across the resistor. (c) Determine the voltage drop across each wire. (d) Often it is assumed the voltage drop across a wire is zero and that it has zero resistance – consider the values in this problem and discuss the validity of this assumption. Under what circumstances is this closest to being true? P.S. The wires described in this problem are not very good wires!
10. Derive a new formula for the resistance of a wire or other material in terms of the length L, resistivity of the substance ρ, mass m, and density D (mass/volume).
11. Resistors of R1 = 68 Ω and R2 = 33 Ω are connected in series and then powered by a battery with voltage 3.70 V. (a) Determine the voltage and current for R2. (b) Repeat if the resistors are connected in parallel instead.
12.
Inspect the
schematic diagram showing a 12 volt battery connected to resistors R1
= R2 = R3 = 100 Ω, and switches
S1 and S2. Determine power for R2
and for the battery for: (a) S1 and S2
both open, (b) S1 closed, S2 open, (c) S1
open, S2 closed, and (d) S1 and S2
both closed.

13.
Consider the
following circuit consisting of four resistors and an ideal battery. (a)
Suppose R1 = R2 = R. Determine the
ratio V1 : V2 : V3 of the
voltages of resistors 1 and 2 compared to either of the others. (b) Determine
the ratio of the powers P1 : P2 : P3.
(c) Now R1 and R2 are changed to particular
values so that the power of each resistor is the same – all four dissipate heat
equally. Determine the values of R1 and R2
in terms of R.

14.
Ideal rechargeable
cells are connected with resistors and a switch as shown. (a) Determine the
rate at which energy is transferred from one cell to the other with the switch
open. (b) Determine the current through the switch in the closed position.
(c) Replace the switch with a resistor of what value to cause the current
through one of the cells to be zero?

15.
Four resistors
are connected in the network shown. Each resistor is 33 ohms. (a) Suppose you
cut one of the wires in the network (at any place) and measure the
resulting resistance across the two loose ends – what is the maximum possible?
Where do you cut? (b) Now suppose instead that you insert a 12 volt battery at
any site you choose to cut – what is the maximum power that can be dissipated
by one of the four resistors?

16. A particular 6.00 V battery has an internal resistance of 1.30 Ω. It is connected to a 100 Ω resistor. (a) How much current flows in the circuit? (b) Determine the terminal voltage (output) of the battery. (c) What is the rate at which the battery itself gives off heat? (d) Repeat if the resistor is 1.00 kΩ instead. (e) Often it is assumed that the voltage output of a battery is the same no matter what. This is true to 3 significant digits as long as the external resistance is greater than what amount?
17. (a) Repeat both parts of problem 11 above, but let the internal resistance of the battery equal 1.10 Ω. (b) Is this much internal resistance still “negligible”? In both circuits? Explain.
18. A student does an experiment to determine the properties of a voltaic cell and measures the potential difference across the terminals to be 1.43 V when the current through the cell is 105 mA and it is 1.39 V when the current is 165 mA. (a) Determine the emf of the cell. (b) Determine the internal resistance. (c) What is the maximum current output possible for this cell and how could it be achieved?
19. When the engine of a car is started a very large current flows from the battery, which has emf = 12.5 V. Suppose the terminal voltage drops to 11.5 V when 130 A runs through the starter motor while cranking the engine. Once the car is started and running the terminal voltage measures 13.8 V because it is being charged by the alternator. (a) Determine the internal resistance of the battery. (b) Determine the rate at which energy is being stored in the battery once the engine is running. (c) Supposing the total capacity of the battery is 75 Ah but it is initially only 20% charged, how long must the engine run to restore it to a full state?
20. A battery with a full charge represents stored chemical energy. (a) Does the rate at which this energy is used for some task affect the total amount of energy that can be “extracted” and used for some purpose? If so, how so? If not, why not? Explain. (b) Follow up your thoughts to this by deriving an expression for the total amount of energy E delivered over the “life” of the battery to an external device of resistance R in terms of the initial chemical energy U, the internal resistance r, the emf of the battery, and appropriate constants. Does this support your response to part (a)?
21. Voltaic cells can be connected in series or parallel to power a device. Suppose an ohmic device of resistance R is connected to three identical cells, each with emf Ԑ and internal resistance r. Compare current delivered to the device depending on type of cell connection. (a) Determine the ratio in the current through the device – cells parallel vs. cells series. (b) Simplify this ratio for the cases: R = 0 and r = 0. (c) What happens to the effective overall internal resistance series vs. parallel? Explain or derive.
22. A capacitor of 150 μF is connected to a 6.0 V battery for a long time. (a) Determine the amount of charge on the capacitor. (b) Determine the energy stored. (c) What voltage battery can be used to store twice the energy in this capacitor?
23. Suppose it is desired to store 1.0 C of charge with a 6.0 V battery. (a) What capacitance is required? (b) The battery will lose how much energy to charge such a capacitor?
24. A doctor calls out “charge to 200!” preparing to use a defibrillator to shock a patient. This means there will be 200 J of energy stored in the capacitor inside the device. “Clear!” yells the doctor holding two electrodes against the patient’s chest. A burst of 40.0 amps flows through the chest, which has resistance 60.0 Ω. (a) Determine the charged voltage of the capacitor. (b) Determine the capacitance. (c) If the current remained constant (which is not true!) how much time would it take to “drain” the charge on the capacitor? (d) If this attempt fails the doctor may repeat and “charge to 300” – what would be the initial current in that case? Would this change the result to part (c)?
25. A capacitor of capacitance C holds a certain amount of energy U and is then connected to a resistance R. (a) Derive an expression for the maximum power output. (b) Assume the power drops linearly with respect to time as the capacitor discharges and sketch a graph of power versus time. Use the area under the curve to derive an expression for the time required for the power to drop to zero. (The result is equivalent to the “time constant”, t.) (c) In reality, the power does not drop linearly and will actually take roughly time 5t to reach zero. Sketch a more realistic power drop curve on the same power vs. time graph.
26. A battery with emf 1.60 V and internal resistance 0.800 Ω is connected to a 470 μF capacitor that is initially uncharged. (a) Determine the initial current. (b) Determine the charge in the capacitor when the current has dropped to one tenth its initial value. (c) Supposing the capacitor gets fully charged, determine the total amounts of energy: lost by the battery, gained by the capacitor, dissipated as heat.
27. A charged 100 mF capacitor is connected to a 120 Ω resistor. The initial current is 0.200 A, but as the capacitor discharges, the voltage and current both decrease. (a) Determine the time constant t = RC. (b) Determine the charge remaining and the current when the voltage has dropped by 40% (to 60% its original value). (c) Use the average current to estimate the time for this drop to occur. (d) Determine the time to drop another 40% (to 60% of the previous value or 36% of the original). (e) Estimate the percentage of the original charge remaining after a time interval of 5t has elapsed.
28.
The switch in
the circuit shown has been open for a long time. The switch is closed at t
= 0 and left in that position for a while. (a) Determine the power of each
resistor at t = 0. (b) Determine the voltage of each resistor long
after t = 0. (c) Determine the amount of heat energy dissipated after
the switch is subsequently opened again. (d) Make a sketch of the current
through the ammeter illustrating the closing and then reopening of the switch.

29. Two capacitors, C1 = 100 μF and C2 = 10.0 μF, are connected to one another and then energized by a 9.00 V battery. (a) Determine the effective capacitance if the capacitors are connected in series. (b) Determine the effective capacitance if the capacitors are connected in parallel. (c) Determine the charge and energy stored in each capacitor for both types of connections.
30.
Consider the
circuit shown below in which the capacitors are all initially uncharged. (a)
Determine the readings of the meters at the instant the switch is first closed
and at a much later point in time. (b) Determine the eventual charge on each
capacitor.
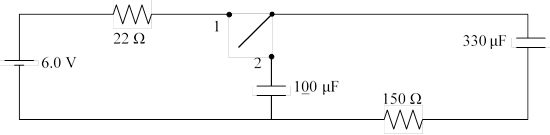
31.
Two capacitors
with no charge are connected in a circuit with the switch initially not
connecting to either position. (a) Determine the initial current when the
switch is moved to position 1. (b) If left in position 1 for a long time, what
is the current just as the switch is moved to position 2? (c) If left in
position 2 for a long time what is the eventual energy stored in each
capacitor. (d) What is the maximum total amount of energy that can be stored
in the two capacitors using this same circuit? And how can this be achieved?

32. A parallel plate capacitor is created using two rectangular metal plates of length and width 10.0 cm by 5.00 cm separated by 1.00 mm of empty space. (a) Determine the capacitance. (b) If the plates are charged to ±25 nC what is the potential difference and electric field strength between the two plates?
33. (a) Starting with the formula for a parallel plate capacitor show that the electric field strength between the plates is given by E = Q/ε0A, where Q is the amount of charge on either plate of area A. (b) The result would seem to imply that the separation distance of the plates is irrelevant. However, this based on a simplifying assumption. The field will be significantly less than the quantity given by this expression if the plate separation is great enough – explain why. (c) The electric field of a capacitor is never completely and perfectly uniform and constant – make a careful sketch of a realistic capacitor field highlighting regions where it most deviates from being uniform.
34. A student is trying to form a capacitor of 1.00 μF using aluminum foil that comes in rolls of width 12 inches and wax paper rolls of the same width. If the thickness of the wax paper is 0.025 mm and has dielectric constant 3.0 what length of foil/wax paper would be required?
35. Two parallel metal plates, each of area 325 cm2 are separated initially by a distance of 1.5 mm. This capacitor is then charged to the fullest extent possible by a battery of 12.0 V. (a) How much charge is on each plate? (b) If the battery is disconnected and then one plate is moved, increasing the separation to 2.0 mm (without changing the amount of charge), what is the increase in potential energy? (c) What external force must act on the plate to slowly move it 0.50 mm? This is equivalent to the amount the plates attract one another. (d) Use Coulomb’s Law to calculate the force of attraction between two point charges equal to that found on these plates and separated by the same distance. Explain the discrepancy.
36. A 3.70 V battery is connected to a parallel plate capacitor that has a slab of insulating material with dielectric constant κ = 4.1 sandwiched between the metal plates. The capacitance with the slab in place is 88 pF. Without disconnecting the battery, the insulating slab is pulled out of the space between the plates. (a) Determine the change in the charge on the capacitor. (b) Does this action increase or decrease the energy stored in the battery? How can this change in energy be explained in light of conservation?
37.
Inserting an insulating
dielectric material between the plates of a capacitor increases the amount of
capacitance. What about inserting a metallic plate with a thickness
less than the separation of the plates? Suppose the original plates are
separated by distance d and then a metallic plate of thickness d/2
is inserted halfway between. Derive an expression for the capacitance with the
extra plate in terms of d, area A, and appropriate constants.
Sketch the field and charge distributions of the three plates.

Selected Answers