AP Physics 1 Assignment – Rotational Mechanics
Reading Chapter 10, Open Stax College Physics; Chapter 9, Etkina
Objectives/HW
|
|
The student will be able to: |
HW: |
|
1 |
Define angular position, angular displacement, angular velocity, angular acceleration and solve related problems in fixed axis kinematics. |
1 – 5 |
|
2 |
Define torque, lever arm (moment arm), and solve related problems. |
6 – 8 |
|
3 |
Define rotational inertia (moment of inertia), use provided formulas of such to solve related problems. |
9 – 11 |
|
4 |
Solve rotational dynamics problems using relation between torque, rotational inertia, and angular acceleration for fixed axis. |
12 – 18 |
|
5 |
Define rotational kinetic energy and work and solve related problems. |
19 – 22 |
|
6 |
Define angular momentum and angular impulse and solve related problems. |
23 – 26 |
|
7 |
State and apply conservation of angular momentum to solve related problems. |
|
|
8 |
Analyze orbital motion, including elliptical orbits, using conservation of angular momentum and energy. |
27 – 30 |
Homework Problems
1. A vinyl musical record is designed to rotate clockwise at 33.3 rpm. (a) Determine the angular velocity in units of radians per second. (b)What is the angular displacement during the 20.0 minutes it takes to play one side of the record? (c) When the turntable is turned off the record continues to turn for 1.50 s before it stops spinning. Find the angular acceleration.
2. While waiting at a stoplight a redneck revs his engine causing the crankshaft of the car’s engine to go from 900 rpm to 3000 rpm in 0.40 seconds. (a) Find the angular acceleration rate of the crankshaft. (b) Determine the angular distance and number of revolutions during this interval of time.
3. Consider a clock on which the second hand moves suddenly from one second to the next in a start and stop fashion. In a very short period of time the hand starts moving and then stops again. Assume that the hand is actually moving for half a second (and then stops for half a second) during each one second. (a) Find the average angular velocity over the course of one minute. (b) Find the maximum instantaneous angular velocity of the hand. (c) Determine the minimum angular acceleration. Hint: model the motion as constant angular acceleration followed by constant angular deceleration; a graph of angular velocity vs. time is helpful.
4. The Ferris wheel at the local fair has diameter 100 feet and a period of 20.0 s once it is moving steadily. (a) Determine the linear speed of the riders. (b) Determine the angular speed of the wheel. (c) If the wheel has angular acceleration 0.100 rad/s2 when it first starts moving, how much time is required to get “up to speed”? (d) Find the angular displacement of the wheel and the distance travelled by the riders during this acceleration.
5. A music record (vinyl) is “played” by a stylus or “needle” that rests in a groove on the surface. As the record turns the stylus spirals inward from the edge toward the center of the record. (a) Given that the angular velocity of the record is constant what happens to the linear speed of the stylus relative to the groove? Explain. (b) A music CD is somewhat opposite from records. A laser “read head” follows a “virtual groove” of reflective pits starting from the center and spiraling outward. Given that the linear speed of the laser relative to the pits is constant what must happen to the angular speed of the CD disk?
6. It takes a certain amount of torque to twist off (i.e. unscrew) the lid of a jar. Given that a person can only exert so much force with their hands and fingers, use physics concepts to explain why both greater diameter and/or a higher coefficient of friction will allow the person to exert a greater torque.
7. A mechanic uses a wrench of length 15 cm in order to tighten a nut. The mechanic exerts a force of 120 N. (a) Determine the maximum torque possible using this much force. In what direction must the force be exerted? (b) Suppose the nut has a torque specification of 25 Nm – the mechanic must exert how much force if using the same wrench? Or use a wrench of what length if applying the same amount of force?
8. A girl of mass 60.0 kg produces torque on the front sprocket (gear) of a bicycle by pushing on the pedals. Each “arm” of the crank has length 170 mm from the axis of rotation of the sprocket to the axis of the pedal. (a) Supposing that the girl “stands” on one pedal (puts all of her weight on it), what is the greatest amount of torque produced? And what is the orientation of the pedal when this occurs? (b) Suppose the pedals are tilted 45° from horizontal and the girl has 80% of her weight on one pedal and 20% on the other – determine the torque.
9. Substitute appropriate SI units into the formula τ = Iα, solve for I and show that the units of rotational inertia are kg m2.
10. The rotational inertia for a point-like object can be found by I = mr2. Three masses, each of 6.0 grams, are placed at x-y coordinates: (0, 0.50 m), (-0.50 m, 0.0), and (0.30 m, -0.40 m). (a) Calculate the total rotational inertia of the three objects rotating about the origin (z-axis). (b) Now calculate the total rotational inertia of a ring of thirty such objects surrounding the origin, all at a distance of 0.50 m. (c) Congratulations! You just found the rotational inertia of a hula hoop of mass 180 g, radius 0.50 m. Explain why the formula I = MR2 can be used to find the rotational inertia of any ring with mass M radius R.
11. Rotational inertia is proportional to mass and radius squared. Given this determine the rotational inertia of each of following in multiples of Earth’s rotational inertia, IE: (a) Jupiter, 320 times more massive, 11 times the diameter; (b) Mars, one tenth the mass and half the diameter.
12. A kid turns his bicycle upside down and then pulls on the tire tread of a bicycle wheel and sets it spinning. The wheel has moment of inertia 0.0940 kg m2 and radius 0.250 m. The wheel has angular acceleration 25.0 rad/s2 CW while the kid is pulling and 0.30 rad/s2 CCW after he releases it. (a) Determine the torque resulting from friction in the axle of the wheel. (b) Determine the torque that the kid exerts on the wheel. (c) Determine the amount of force that he must have exerted to start it spinning.
13. A gyroscope with rotational inertia 9.0 × 10–5 kg m2 is set into motion by wrapping a string around its axle and then pulling the string. The rate of spinning increases as the string unwinds off the axle of diameter 3.0 mm. Given the string is 40.0 cm long and the tension is 3.0 N as it unwinds determine: (a) the angular acceleration, and (b) the final angular speed.
14. A yo-yo has a moment of inertia that can be modeled by I = ½ MR2. When a yo-yo is “sleeping” its axle, radius r, is spinning inside a loop at the end of the string. Suppose the yo-yo is initially spinning with a period T and is “sleeping” in a loop with coefficient of friction μk. Derive expressions for the time t it takes for the yo-yo to completely stop and the number of revolutions n it will make during this time.
15. Two kids sit on either side of a seesaw, which is in a horizontal position. The seesaw has rotational inertia 17.0 kg m2 and is balanced about its pivot point. If one kid is 50.0 kg, seated 1.6 m to the left of center, and the other kid is 40.0 kg, seated 1.7 m to the right of center, what is the angular acceleration of the system? Use I = mr2 to determine how much rotational inertia each kid adds to the system.
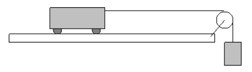
16. A pulley of mass 20.0 g
and radius 3.00 cm is used in a physics experiment as shown. Its
rotational inertia is given by I = ½ MR2.
As the cart accelerates, the tension in the string on the cart side of the
pulley is 0.438 N and on the other side of the pulley it is 0.446 N. (a)
Find the angular acceleration of the pulley. (b) Determine the
acceleration rate of the cart/hanging mass system. (c) If the same
experiment is done with a pulley of the same radius but mass 5.0 g what will be
the difference in the tension on either side if the acceleration is the same as
before?
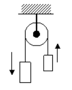
17. An “Atwood’s machine”
with masses of 0.40 kg and 0.70 kg hanging on either end of the string is shown
in the diagram below. The pulley has moment of inertia 0.0015 kg m2
and radius 0.10 m and angular acceleration 20.0 rad/s2 when the
masses are released. (a) Determine the linear acceleration of each mass
assuming the string does not slip on the pulley. (b) Find the tension on
each side of the pulley. (c) Determine the torque on the pulley due to
friction. (d) What would be the acceleration of the masses if the pulley
is “massless” and “frictionless”? (i.e. maximum possible
acceleration given “best” pulley)
18. A spinning top slows down because of friction. (a) The design of the top can lead to longer spins by giving it a very narrow tip upon which to balance and spin. Explain why the small radius of the “point” of contact helps to prolong the spinning of the top. What would happen if it were truly a point of contact (with zero radius)?! (b) Designing the top to have a relatively large rotational inertia can also help to prolong its spinning. Explain. Describe two ways the rotational inertia can be increased by the way the top is manufactured.
19. An object of mass 6.0 kg moves at constant speed 5.0 m/s in a circular path of radius 2.0 m. (a) Calculate its kinetic energy by using K = ½ mv2. (b) Calculate the object’s angular speed and rotational inertia. (c) Calculate its kinetic energy by using K = ½ Iω2.
20. A regenerative braking system stores kinetic energy of a car so that it can be recovered when the vehicle resumes moving. One way to do this is to “store” the energy in a spinning flywheel. One such design uses a solid disk flywheel with moment of inertia 0.040 kg m2 and maximum rotation rate 45000 rpm. (a) What is the maximum energy storage? (b) In principle it could store the kinetic energy of a 1700 kg car moving at what speed before braking? (c) If this energy is used to start the car moving again in 10.0 s, what is the power output of the system?
21. A bicycle and its rider have total mass 90.0 kg and coasts initially at 5.00 m/s. Each wheel has mass 2.1 kg and radius 0.32 m and moment of inertia approximated by I = ¾ MR2. (a) Determine the rotational kinetic energy of each wheel when moving at this speed. (b) What percent of the bicycle’s total kinetic energy is the rotational energy of the wheels? (c) Ignoring friction, determine the final speed of the cyclist if he coasts without pedaling down a hill of height 3.00 m and length 20 m.
22. A certain toy “helicopter” or “whirlybird” consists simply of a propeller attached to a shaft that is spun rapidly by hand to a certain angular speed ω0 and then released. The spinning propeller/shaft flies upward as the angular speed of its turning decreases. The propeller and shaft each have length L and mass m and the propeller has moment of inertia 1/12 mL2. (a) Based on conservation of energy derive an expression for the maximum height the toy could possibly attain in terms of the given quantities and appropriate constants. (b) The observed maximum height of such a toy would be substantially less than this – explain.
23. A wheel with rotational inertia 0.80 kg m2 has initial angular speed 7.0 rad/s. It slows to a stop because of friction, completing 6.5 revolutions in the process. (a) Find the initial kinetic energy and angular momentum. (b) Use kinetic energy to find the torque due to friction in the axle of the disk. (c) Use the angular momentum to find the external angular impulse acting on the wheel that would accelerate it back to the same speed in 0.50 seconds?
24. At a playground a kid of mass 70.0 kg stands at the center of a rotating “merry-go-round” with rotational inertia 975 kg m2 and angular speed 1.5 rad/s. The kid walks outward and stops at a distance 1.6 m from the center of the rotating platform. (a) Find the resulting angular speed. (b) Find the change in kinetic energy of the system. Use I = mr2 for the kid and ignore friction.
25. Same playground, same kid, same merry-go-round as previous problem. Suppose the kid comes running north at 3.0 m/s along a tangent path and jumps on the platform, which is initially at rest. The tangent path and the spot where he lands is 1.4 m from the axis. (a) Find the resulting angular speed of the system. (b) If the kid jumps off again, this time moving south at 2.0 m/s, what will be the final angular speed of the platform?
26. An ice skater of mass 75 kg and height 1.7 m is spinning with his arms stretched wide at a frequency of 1.1 Hz. He then pulls his arms in next to his body, causing his rotation rate to increase. Use rotational inertia models: I = 0.019 mh2, arms stretched wide; I = 0.010 mh2, arms next to body. Ignore friction. (a) Find the initial angular momentum and kinetic energy. (b) Find the frequency of rotation once his arms are brought in. (c) Determine the work done by the skater to perform this feat.
27. The distance from the Moon to the Earth is increasing at a rate of about 3.8 cm per year. Determine the torque acting on the Moon by taking the following steps: (a) Derive an expression for the angular momentum of a circular orbit as a function of radius. The result should be L in terms of G, Mearth, mmoon, r. (b) Use the expression and appropriate numerical values to calculate the rate of change in the angular momentum, recognizing that the result is equivalent to the torque acting on the Moon. (c) This torque is due to a complex gravitational interaction associated with the tides, but it must obey the principle of Newton’s 3rd Law. Use this fact to find the change in the length of one day that occurs in one year, given the Earth’s rotational inertia is 8.01 × 1037 kg m2. Note: this calculation requires the use of many digits – preferably done on a calculator with at least 12 digit precision – do not round off intermediate results!
28. An elliptical orbit can be analyzed using conservation of angular momentum and mechanical energy. The distance between Earth, mass 5.972 × 1024 kg, and Sun, mass 1.989 × 1030 kg, varies from 147 to 152 Gm. (a) Use the formula UG = – Gm1m2/r to find the change in potential energy that occurs moving from the farthest distance to the nearest. (b) Given that the speed of Earth at its farthest point is 29.29 km/s, use conservation of energy to find its speed at the nearest point. (c) Calculate the angular momentum of Earth at each extreme and show that it is equal.
29. Use concepts from the previous problem to find the speed of Pluto at each extreme of its orbit about the Sun – distance varying from 4.44 × 1012 m to 7.38 × 1012 m. Hint: use a system of equations based on conservation of energy and angular momentum.
30. Stax College Physics
Problems & Exercises found at end of sections 10.2 – 10.6
Etkina, pp. 278 – 283, Chapter 9: 25, 31, 33, 35, 47, 56, 57, 60, 67
Selected Answers