AP Physics 1
Assignment - Kinematics
Reading Chapter 2, Open Stax
College Physics; Chapter 2, Etkina et. al.
Objectives/HW
|
|
The student will be able to: |
HW: |
|
1 |
Define and distinguish the concepts scalar and
vector. Make the connection
between the visual representation of a vector and its numerical
representation of magnitude and direction angle. |
|
|
2 |
Define, distinguish, and apply the
concepts: distance, displacement,
position. |
1,
2 |
|
3 |
Define, distinguish, and apply the
concepts: average speed, instantaneous
speed, constant speed, average velocity, instantaneous velocity, constant
velocity. |
3
– 7 |
|
4 |
Define, distinguish, and apply the
concepts: average acceleration
and instantaneous acceleration, and constant acceleration. |
8
– 16 |
|
5 |
State the displacement and velocity relations
for cases of constant acceleration and use these to solve problems given
appropriate initial conditions and values. |
17
– 27 |
|
6 |
State and apply to applicable scenarios the
conditions of freefall, including the value of g, and solve related
problems. |
28
– 39 |
Homework Problems
1.
Suppose you buy a new car and its
odometer shows 15 miles. However,
the displacement of the car since it was first manufactured may be hundreds or
even thousands of miles. (a) Does
the odometer show the true distance traveled by the car since it was
manufactured? Explain. (b) Suppose that on a future date the
odometer shows 100000 miles but the displacement is actually zero – what
would cause this? Explain.
2.
Assume the field in Neyland
Stadium runs perfectly north and south.
Beginning with an initial position of 60.0 yds. , 90.0¡ from the south
goal post, Mr. M marches (in linear segments) the following four displacements
in succession: d1
= 10.0 yds, 0.0¡,
d2 = 11.2 yds, 206.6¡, d3
= 11.2 yds, 333.4¡,
d4 = 10.0 yds, 180.0¡. (a) Using a protractor and ruler measure
and construct a scale diagram of Mr. M's march. (b) From initial to final position what
is the overall displacement? (Hint:
measure your diagram!) (c) From
initial to final position what is the total distance? (d) What is the final position?
3.
The speed of light in the vacuum of space
or in air is a constant value of 3.00 × 108 m/s.
(a) Calculate the distance traveled by light in one yearÕs time (known as a
Òlight-yearÓ).
(b) What amount of time does it take for light to travel from the Moon to the
Earth – a distance of 384 Mm?
(c) How much time would it take a car traveling 45 m/s (100 mph)?
4.
An airport radar uses the reflection (or
"echo") of a radio signal to measure aircrafts' positions. Suppose the position of a certain
helicopter at 1:00 PM is 105 miles, 90.0¡
from the airport. At 1:30 PM it is
48 miles, 90.0¡
from the airport. (a) Find the
displacement of the helicopter over this interval of time. (b) Find the average velocity of the
helicopter.
(c) If the velocity remains constant what will be the position of the
helicopter at 1:45 PM? Note: a diagram showing the airport and
helicopter is very helpful!
5.
You are driving down a street in a car at
85 km/h. Suddenly a deer darts into
the street. If it takes you 0.75 s
to react and apply the brakes, how many meters will you travel before you begin
to slow down?
6.
Suppose you need average speed of 100
km/h to arrive at a certain destination on time. However traffic limits your average
speed to only 60 km/h during the first half of the tripÕs distance. (a) What must your average speed be in
the second half of the trip to be on time?
(b) Regardless of how fast you drive in the second half you can only
improve your overall average speed so much. Determine the greatest possible average
speed for the entire trip – derive and/or explain.
7.
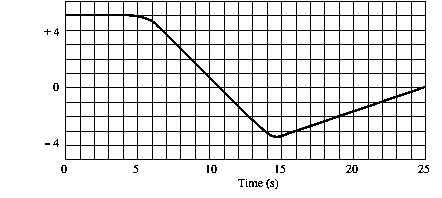The
graph below shows the motion of a hummingbird. For the interval of time shown,
determine the following: (a) Determine
the time and position when the bird is farthest west of the flower. (b) Determine the birdÕs average
velocity. (c) Determine its average
speed. (d) What is the birdÕs velocity at 10.0
s? (e) Determine the speed at t = 5.5 s, and explain whether it is
increasing, decreasing, or constant at that point. (f) At what position(s) is the birdÕs
velocity equal to zero? (g) What is
the birdÕs maximum speed?
8.
An airplane is accelerating along a
linear flight path and has average velocity 400 mph, north from 1:00 pm to 1:02
pm. The planeÕs instantaneous speed
may or may not be equal to 400 mph at 1:01 pm. Make a careful sketch of a distance vs.
time graph (showing these two minutes of flight) illustrating three
possibilities: the instantaneous speed
is less than, greater than, or equal 400 mph at 1:01 pm.
9.
A 1956 VW Van could go from 0 to 60
mph (26.8 m/s) in 75 seconds (as measured by Road & Track). (a) Determine the average rate of
acceleration. (b) Assuming a
braking deceleration of 9.0 m/s2 what amount of time was required to
return from 60 mph to 0?
10. In
the 1940Õs rocket-powered sleds were used to test the responses of humans to
acceleration. Suppose the sled reaches
a speed of 222 m/s in 2.10 s and then in another 0.90 s is brought to a stop. Determine the greatest number of g's
(in any direction) experienced by the rider. (A "g" is an
acceleration rate equal to 9.80 m/s2.)
11. An
F-22 fighter jet is flying at a ÒsupercruiseÓ speed
of 545 m/s when the pilot kicks in the afterburners. The afterburners cause an acceleration
rate of 3.47 m/s2. How
much time is needed to reach a speed of 600 m/s (Mach 2.0 or twice the
speed of sound!)?
12. A
baseball with an initial velocity of 40.0 m/s, south undergoes an average
acceleration of 1.15 ×
105 m/s2, northward due to the impact of a bat that is in
contact with the ball for 0.75 milliseconds. What is the final velocity of the ball?
13. A
2010 Chevy Camaro went from zero to 20 mph, 40 mph, and 60 mph, in times of 1.1
s, 2.6 s, and 4.6 s respectively.
This is an interesting pattern because the average acceleration changes
by about the same percentage for every 20 mph faster the car goes. (a) By about what percent does the
acceleration rate change per every 20 mph increase? (b) If the pattern continues, what time
is required to go from 0 to 80 mph?
14. Answer
the following and explain or give an example: (a) Can an object have a speed equal to
zero and at the same time an acceleration not equal to zero? (b) Can an object have a constant speed
and a changing velocity? (c) Can an
object have a constant velocity and a changing speed? (d) Can an object be moving but not
accelerating? (e) Can an object
have velocity and acceleration vectors that point in opposite directions?
15. 
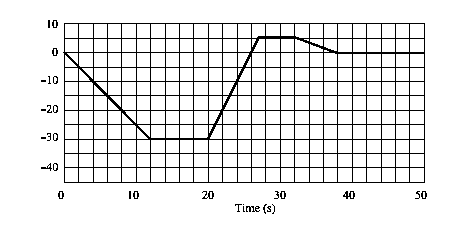The
graph below shows the motion of an object.
For the interval of time shown, determine the following: (a) At what
point(s) in time is the object moving southward? (b) Find the maximum speed. (c) Find the average acceleration from t
= 16 s to t = 32 s. (d) Find
the acceleration at t = 4.0 s and state whether speed is increasing or
decreasing at that point. (e) Find
the acceleration at t = 26 s.
(f) The acceleration is zero at what point(s) in time? (g) The speed of the object is
decreasing at what point(s) in time?
16. Using
the same graph (shown above), determine the displacement of the object during
the following intervals of time:
(a) from 0 to 12 s, and (b) from 20 to 32 s. (c) Determine the distance traveled by
the object from 0 to 50 s.
17. A
skateboarder starts from rest atop a slope that is 20.0 m long and accelerates
uniformly 2.60 m/s per second down the slope. (a) What is the position of the
skateboarder 3.00 s later? (b) What
is the speed at that point? (c) How
much time overall is needed to go down the slope?
18. You
are investigating an accident scene in which several cars wrecked in order to
avoid a car skidding to a stop. The
skid marks are 65 m long. A
skidding car will have a deceleration rate of about 10 m/s2. How fast was this car going before it began
to skid?
19. An
object traveling on a horizontal surface with an initial velocity of 12.0 m/s
to the right is then accelerated 3.00 m/s2 towards the left. (a) Calculate the magnitude of this
object's displacement at values of time:
0.00, 4.00, and 8.00 s. (b)
Calculate the speed for the same times.
(c) Describe the motion of the object for this time interval.
20. At
t = 0.00 s a ball is started rolling
up an inclined plane with an initial velocity of 6.00 m/s, 15.0¡. At t
= 2.00 s the ball reverses its direction and begins to roll back down. (a) How far up the slope does the ball
travel? (b) Find the ball's
acceleration. (c) Find the speed of
the ball at t = 3.00 s. (d) Find the distance traveled by the
ball during these 3.00 seconds. (e)
Find the ball's position at t = 3.00
s.
21. An
object with constant acceleration travels a distance d in amount of time t. Derive expressions in terms of d and t for: a, the magnitude of its acceleration, and
vmax,
the maximum speed, in two cases:
(a) its initial speed is zero, and (b) its final speed is zero.
22. (a)
Determine the displacement of a plane traveling northward that is uniformly
accelerated from 66 m/s to 88 m/s in 12 s.
(b) Repeat the calculation for the same plane slowing down from 88 m/s
to 66 m/s in 12 s and show that the result is the same.
23. The
bullet leaves the muzzle of a Glock 17 pistol with a speed of 375 m/s. The barrel of the pistol is 11.4 cm
long. Find the acceleration rate of
the bullet passing through the barrel.
24. A
moving car decelerates for 5.0 s and comes to a complete stop. It travels 75 m in the process. (a) Determine its initial value of
speed. (b) Determine its rate of
deceleration.
25. The
driver of a van Òtimes the lightÓ and passes through an intersection at
constant speed 15.0 m/s just as the light turns green. At the same time a car in the adjacent
lane accelerates from rest at 3.0 m/s2. (a) What distance must the car travel in
order to catch up to the van (and then pass)? (b) What is the speed of the car as it
passes the van?
26. An
object moves along a linear path with constant
acceleration. Show mathematically
that the average velocity of this
object over any interval of time is equal to the instantaneous velocity at a point exactly halfway through that
interval of time. Would this be
true if the acceleration is not
constant?
27. A
driver of a car going 25.0 m/s suddenly notices a stop sign 40.0 m ahead. The braking deceleration rate of the car
is 10.0 m/s2, but it takes the driver 0.75 s (reaction time) to get
the brakes applied. (a) Determine
if the car runs the stop sign. (b) Determine
the maximum initial speed at which the car could be moving and manage to stop
at the sign.
28. Under
what circumstances is the effect of air resistance negligible on a falling
object?
i.e. When is the use of g = 9.80 m/s2
most valid?
29. One
rock is dropped from a cliff, a second rock is thrown downward. When they reach the bottom, which rock
has a greater speed? Which has a
greater acceleration? Which reaches
the ground in the least amount of time?
30. A
stone is dropped into a very deep hole in the ground and it hits the bottom
after falling for 2.80 s. (a) How
deep is the hole? (b) What is the
impact velocity of the stone?
31. Suppose
a person drops 20.0 m (about 5 floors) from a burning building and onto an air
bag. (a) What will be the person's
maximum speed during their fall?
(b) Repeat for a drop of 40.0 m.
32. A
ball is thrown upward with an initial speed of 15.0 m/s. (a) Find the maximum height attained by
the ball. (b) How much time does it
take to reach the maximum height?
How much time does it take to fall back down? (c) What is the ball's velocity when it
reaches its initial position?
33. A
punter goofs and punts the football straight up. The hang time (total time in the air) is
4.00 s. (a) What height does the ball reach? (b) What initial velocity in miles per
hour does the ball have?
34. A
space explorer lands on a certain planet and does an experiment to measure the local
gravity. She launches an object straight upward and observes
that it takes a total time T to return to the launch point and attains a maximum height h
above the launch point. Derive an expression for the value of g
on this planet in terms of h and T and any appropriate constants.
35. A
juggler throws a beanbag straight up into the air with initial speed 6.00
m/s. The beanbag leaves the
juggler's hand 1.50 m above the floor.
The juggler fails to catch the beanbag as it falls to the floor. (a) How long is the beanbag in the
air? (b) What is its impact speed?
36. Someone
in a skyscraper drops an egg on the bossÕs car. The boss is mad. He asks you to investigate. You discover that a running video camera
in the building recorded the egg passing by a 20th floor full-length
window that is 3.00 m from ceiling to floor. Reviewing the tape you notice it takes
0.20 s for the egg to pass the window.
Each ÒstoryÓ or ÒfloorÓ of the building is 4.00 m. (a) From how high above the top of the
window was the egg dropped? (From which floor?) (b) With what speed did the egg hit the
carÕs roof? (which was level with the floor of the 1st floor)
37. A
tennis ball is dropped from 1.20 m above the ground. It rebounds to a height of 1.00 m. (a) With what velocity does it hit the
ground? (b) With what velocity does
it leave the ground? (c) If the
ball were in contact with the ground for 0.010 s find its acceleration while
touching the ground. (i.e. the acceleration of the
"bounce")
38. Choose
and solve one of the problems from either text:
Open Stax College Physics Problems & Exercises
found at the end of sections 2.5, 2.7, or 2.8
Etkina pp. 45 – 50: Chapter 2, Problems 18, 26, 28, 35, 46,
53, 62, 74, 79, or 85
39. Choose
and solve another one of the problems listed above.