AP Physics 1 Energy& SHM Lab
The purpose of this investigation is to verify the concepts of Conservation of Energy and Simple Harmonic Motion. This will be accomplished by hanging a mass from a spring and allowing it to oscillate vertically. In the absence of nonconservative forces such as friction, the energy of the mass-spring system should remain constant. Force will be measured by a force sensor from which the spring hangs. The oscillation of the mass will be measured by a motion detector resting directly beneath. The sensors are connected to Vernier Graphical Analysis running on a Chromebook. The same app (or other software) is used to graph and interpret the data and create an energy graph of the elastic, gravitational, and kinetic energy of the mass-spring system.
Procedure
Connect two ring stands with a right angle clamp. Attach a force sensor to the end of the horizontal metal rod and support it rigidly on the table. The force sensor should extend beyond the edge of the table. The motion detector will be placed directly below the force sensor. A spring will be hung from the force sensor and a mass from the bottom of the spring. IMPORTANT: Great care must be taken not to drop a mass on the motion detector!! It would be a good idea to always move the motion detector to a safe location and put it below the mass ONLY during the very brief interval of time when it is actually in operation!
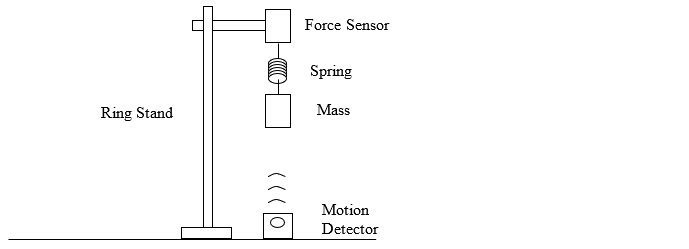 |
1. Connect both sensors to the laptop and Graphical Analysis using either USB cable or Bluetooth. Suggestion: the wired connections may be more reliable.
2. Under Data Collection Settings set the length of the experiment to only 3.00 seconds.
3. To calibrate the force sensor you will enter two known values of force acting on the sensor. Read the next two steps before you proceed with the calibration.
4. Move the Motion Detector to the side and then hang only the spring from the sensor. Click on the Force button and Calibrate. Then enter zero as the First Known Value and click Keep. This means that the computer will record zero newtons for force when the spring is in this condition and it is not exerting any force on the test object.
5. Before entering the Second Known Value hang the test object on the end of the spring and find the position at which it will rest without accelerating. Use the mass to calculate and enter the correct weight (in newtons!) of the test object (not including the spring!) and click Keep. This means that the computer will record a force equal to the weight of the test object when the spring is in this condition and is exerting that much force on the test object. All other readings from the sensor are now adjusted according to the two known force values that have been entered by you – this is done by the program.
6. Check that all of the support structure is very secure. Keep the motion detector out from underneath the mass. Carefully lift the mass upward and let it go so that it bobs up and down with an amplitude of about 10 cm. Do not pull downward and release because this may “launch” the mass!
7. Once the mass is already in motion and oscillating smoothly, then place the motion detector directly below it and click on the Collect button.
8. This should produce smooth graphs showing fluctuations of position and force with respect to time. If there are any significant glitches in these graphs then make adjustments and repeat the experiment.
9. Remove the motion detector to a safe location whenever you are not actually collecting data.
10. Under the File menu use the Save command to save your data.
Analyses
Use a computer to produce graphs of Position vs. Time, Force vs. Position, Force vs. Acceleration, and Energy vs. Time, with curve fits and statistics where appropriate. There are many ways to do this – step by step directions are given below, but you are free to use other means. The quality of the resulting report and graphs matters and will be graded!
A complete report (50 pts): (pages in this order)
q Data Table Sample (show all columns but not necessarily all rows) (6)
q Position vs. Time graph, with regression equation. (6)
q Force vs. Position graph, with regression equation. (6)
q Force vs. Acceleration graph, with regression equation. (6)
q Energy vs. Time graph (K, Ug, Us, and E), with statistical analysis of total energy (6)
q Energy vs. Position graph (K, Ug, Us, and E) (6)
q On separate paper, responses to the questions. (14)
Using Vernier Graphical Analysis on Chromebook
You have much control over the appearance of graphs – single click, double click, or right click when you want to change something! Search the menus found in the corners the pane(s).
General tips using the application:
1. The program has multiple viewing “windows” – click on the View Options button in upper right corner to choose what is displayed.
2. Under the File button in the upper left corner there are options to Export your work. When you choose to export Graph Image it creates an image file (.png) of whatever graph or graphs that are currently being displayed. Suggestion: work on one graph at a time and then export to an image file that can be put into Microsoft Word, Google Docs, etc. Also you may want to save the Graphical Analysis file by using Save As and give it a unique name for each graph you create. By saving many versions of the file you can more easily go back and correct or make changes if necessary.
3. The other Export option is Comma-Separated Values. Use this option to save the completed data table in a form that can be opened by other programs such as Microsoft Excel, Google Sheets, etc. You can use this feature if you want to produce the graphs using an application other than Graphical Analysis.
4. Except
for the energy graphs, all other graphs should be adjusted as follows:
Under Graph Tools, choose Apply Curve Fit. Choose an appropriate
model. When doing a curve fit you may choose to select and analyze only a
portion of the graph and data if it results in a more legitimate match between
the data and the curve or line generated by the equation. (However, this may
not be necessary.)
Under Graph Tools and Graph Options choose Points but not
Lines – whenever a curve fit is shown, the data points should be shown as a
scatter plot (no connecting lines). Also adjust the y-axis range as
necessary to produce the best looking graph. The equation should not cover the
data. You can also adjust the x-axis range. It is essential that all
data be showing! And give the graph an appropriate title.
Position vs. Time, Force vs. Acceleration, and Force vs. Position:
5. Position vs. Time graph: use a sine model curve fit.
6. Force vs. Position graph: Click on the x-axis label (Time) and change it to position. Use a linear model.
7. Force vs. Acceleration graph. Change the x-axis to Acceleration. Use a linear model.
Energy vs. Time, Energy vs. Position, and Data Table:
8. Now you will need to add columns to the data table. The goal is to have the computer calculate and graph the energy of the system. It will be convenient under View Options to choose to show graph(s) and the data table at the same time. Click on the three dots at the top of a column in the table to access Column Options and Add Calculated Column. When you add a column it will be inserted immediately to the right, so choose where you want to insert it.
9. Under Add Calculated Column enter an appropriate name and units and then choose an expression type that can be used for the desired operation. For this lab you can use A*X^B, A*X+B, and A*X+B*Y to achieve all necessary calculations. Or if you are using the “Pro” version you can use the Custom Expression option. The directions below explain how to use the “built in” functions.
10. Add a Height column: the h in mgh will be the height above the lowest point in the oscillation. Use the position vs. time graph to determine the lowest position measured by the motion detector. Then use the expression A*X+B to produce the column of height values. For example, if the lowest position were 0.60 m, then you could let A = 1, X = Position, and B = –0.60 to calculate height.
11. Add an Elongation column: the x in ½ kx2 is the amount the spring is stretched. This is the difference in the mass’s measured position and the position at which the force of the spring is zero. Use the linear regression from force vs. position to solve for the position at which the force of the spring is zero. Then use the expression A*X+B to produce the column of elongation values. For example, if the linear regression indicates the force equals zero at a position of 0.85 m, then you could let A = –1, X = Position, and B = 0.85 to calculate elongation.
12. Add a Kinetic Energy column: use the expression A*X^B. The value of A should be half the mass of the object. (What should X and B equal? You should know!)
13. Add a Gravitational Energy column: use the expression A*X^B. The value of A should be the weight of the object. (What should X and B equal? You should know!)
14. Add an Elastic Energy column: use the expression A*X^B. The value of A should be half the value of the spring constant k – determine k from the linear regression of force vs. position. (What should X and B equal? You should know!)
15. Add a Potential Energy column: use the expression A*X+B*Y. X and Y are the two types of potential energy.
16. Add a Total Energy column: use the expression A*X+B*Y. X and Y are potential and kinetic energy. This final column is the sum of all three types of energy present in the mass/spring/earth system.
17. Make a graph of Energy vs. Time showing all forms (K, Ug, Us, and E). Make sure there is a legend on the graph. For this graph plot Points and Lines – “connecting the dots” helps illustrate the trends in the variables. There will be no regression equations on this graph. Instead, do a statistical analysis of the total energy by clicking on the View Statistics option under Graph Tools - scroll through the statistics box until you find the information for the total energy. Adjust the overall appearance as necessary – for example, the legend and the statistics boxes should not cover significant features of the graph.
18. Make a graph of Energy vs. Position showing all forms (K, Ug, Us, and E). Adjust as necessary. Note: you do not need to repeat the statistics on this graph because it will be the same result.
Questions
1. Highlight or otherwise indicate one row from the data table and check the computer’s calculations by doing them yourself: calculate kinetic energy, gravitational potential energy, elastic potential energy, and total energy. Show your work!
2. Discuss whether or not your results support Conservation of Energy and explain how so. Refer specifically to one or more graphs.
3. Discuss
whether or not your results support the concepts of Simple Harmonic Motion:
(a) Refer to the Force vs. Position graph and describe specifically whether it
shows that the object was under the conditions that cause SHM.
(b) Refer to the Position vs. Time graph and describe specifically whether it
shows the object exhibited the expected type of motion associated with SHM.
(c) Use the appropriate coefficients from the regression on the Position vs.
Time graph to identify and write down the equilibrium position and amplitude.
Showing your work, plug the equilibrium position into the regression from the
Force vs. Position graph and calculate the amount of force – does the result
make sense? Explain.
4. Show
work as you:
(a) Use an appropriate coefficient from the regression on the Position vs. Time
graph to determine the period of the object’s motion. Show your work.
(b) Use your values for k and m to calculate the theoretical
period.
(c) Calculate the percent error, taking the first value (from the Position
graph) to be the most likely actual “true” period.
5. Consider
the regression equation of the Force vs. Acceleration graph:
(a) Explain how it is consistent (or not) with Newton’s Laws – be specific.
(b) What is the significance of the slope? the y-intercept?
(c) Make any appropriate calculation(s) such as error or deviation that will
quantify the accuracy and/or precision of the slope and/or y-intercept.
6. Use the statistical results on the Energy vs. Time graph to determine the percent deviation in the total energy of the mass-spring system. (The standard deviation is what percent of the mean?) This indicates the average fluctuation in the total energy
7. Write an intelligent, grammatically correct paragraph or two discussing both the signs of error and the likely sources thereof.