Measurement - Unit Notes

Find below a summary of important concepts, definitions, and skills that will be used throughout the year in this course. You may have encountered much of this material in other classes that you have taken previously.

Uncertainty in Numerical Values

Physics involves many mathematical concepts and being able to work with numbers and equations is an essential skill. With very few exceptions, when we represent some aspect of the world around us with a numerical value there will be at least some amount of uncertainty. In other words almost all meaningful numerical values are impossible to know perfectly and will contain a certain level of error.

Exact Numbers

A numerical value that is known to be completely accurate and which contains no conceivable error is said to be exact. An exact number is one for which every digit is known or knowable with absolute certainty.

Examples:

Certain mathematical constants: π = 3.14159265359…, e = 2.71828182846…, etc.

Certain constants in equations: A = ½ bh (the ½ is exact), C = 2πr (the 2 is exact), etc.

Counted values (so long as it is a relatively low number): for example there are exactly

50 stars on the American flag, or exactly 5 toes on one foot

Some unit conversions, such as: 1 m = 100 cm, 1 inch = 2.54 cm, 1 minute = 60 s, etc.

Certain physical constants: c = 299792458 m/s, h = 6.62607015 × 10⁻³⁴ Js, etc.

Standards of measure, such as: 1 meter = distance traveled by light in 1/299792458 s,

1 second = 9102631770 oscillations of a certain radiation from cesium atoms, etc.

Inexact Numbers

Essentially all other numerical values in physics besides those listed above are either measures or estimates of physical amounts or quantities. Such a value will always have a level of uncertainty. Take for example the length of a table. If you measure the table with a ruler you can only get to the nearest tenth or perhaps hundredth of a centimeter – all decimal places beyond the last measured digit are unknown. With a better measuring device you might get the length of the table to the nearest thousandth of a centimeter. But no conceivable measuring device can determine the exact length of the table. Besides measuring, how else can we obtain a value for the length of the table? We could estimate it – but that obviously has uncertainty. We could use the value for the length that comes from the manufacturer – but the only way the manufacturer can be sure of the length is to measure it and then we are back to square one. Therefore we can say that there is no way to know the exact length of a table (except to define the length and use the table as a new standard by which all other lengths are judged – but, hey, its just a table :). The same ideas apply to any length (not just tables). And the same ideas apply to other quantities besides length, such as: time, mass, volume, pressure, temperature, etc. The long and short of it is that almost all numerical values used in physics are inexact and have some amount of uncertainty! This is simply a “fact of life” and scientists must “deal with it”.

Accuracy and Error

Accuracy is the closeness of a numerical value to its accepted or “true” value. The closer to the “correct” numerical value, the more accurate is the result. When a scientist measures a well-known quantity, such as the speed of light or the density of copper, he or she can find the value in a reference book and determine the extent to which the result is accurate. We shall call such a reference book value the “accepted value” because the scientific community has accepted it as true and correct. However, for other quantities such as the length of a table there is no accepted value and there is no simple way to determine the amount of accuracy.

The numerical error is the difference between a measured value and the accepted value. The error is usually given in “absolute” terms, which means that the absolute value of the difference is taken. Often error is expressed as a relative (percent) value. By calculating error we can quantify accuracy – the smaller the error, the more accurate is the result.

absolute error:

relative or percent error:

where: x = a measured or experimental value

x_o = the accepted or true value

Example:

A student measures the density of lead and has a result of 10.5 g/cm³. However, the accepted value for the density of lead according to a periodic table is 11.4 g/cm³. The absolute error in the student’s result is found by calculating: |10.5 – 11.4|. Therefore the absolute error is equal to 0.9 g/cm³. The relative error is found by calculating: 0.9/11.4. Therefore the relative error is equal to 8%. For lab work done at the high school level this would be a reasonably accurate result – most of our equipment can produce results with error of 10% or less when used with care.

Precision and Deviation

Precision is a bit harder to define – there are two common uses of the word in science. If a quantity is repeatedly measured to form a set of values we can say that precision is the extent to which the values in the set are in agreement. The closer the repeated measures are to one another, the more precise is the set of values. In other words, precision is an indication of the “repeatability” of the results. A different usage of the word precision involves a single measurement of a quantity. In this case we can say that precision is the amount of exactness in the measure. The smaller the divisions of measurement and the more digits that can be established the more exact and more precise is the value.

Deviation is the difference between a single measured value within a set and the mean of that same set. Like error, this is usually done in absolute terms. And once again it may be expressed as a relative (percent) value. By calculating deviation we can quantify precision – the smaller the deviation, the more precise is the result.

absolute deviation:

relative or percent deviation:

where: x = one measured or experimental value from a set

= the mean of the set

Example:

The length of a table is measured repeatedly producing the following set of five values: 123.4 cm, 123.9 cm, 122.9 cm, 123.5 cm, and 123.2 cm. The mean or “best value” of this set is 123.4 cm. The absolute deviation of each value in the set is found by subtracting the best value and results in the following: 0.0 cm, 0.5 cm, 0.5 cm, 0.1 cm, and 0.2 cm. These values can be averaged to find the mean absolute deviation of 0.3 cm. We could summarize the measurement of the length of the table by reporting the best value and the average absolute deviation: 123.4 cm ± 0.3 cm. Note: scientists normally use “standard deviation” but you will not be required to do so in this course.

Systematic and Random Error

A source of error that causes results to be sometimes high and sometimes low (compared to the “true” or accepted value) is said to be a random error. Random error is characterized by roughly equal amounts of “scattering” on either “side” of the true value. Greater amounts of random error result in more deviation and less precision. However, random error will not much affect the accuracy of the mean or average of a set of measures.

A source of error that causes results to be consistently higher than the true value or consistently lower than the true value is said to be a systematic error. Systematic error is characterized by “skewed” results that are preferentially to one “side” of the true value. Greater amounts of systematic error result in greater numerical error and less accuracy of the mean or average of a set of measures. However, systematic error will not affect deviation or precision

A good way to visualize the above ideas is with the help of a time-honored analogy. Making a measurement is a little like throwing darts – getting closer to the true or accepted value is like getting closer to the bull’s-eye. Consider the four patterns of shots at a bull’s-eye shown below.

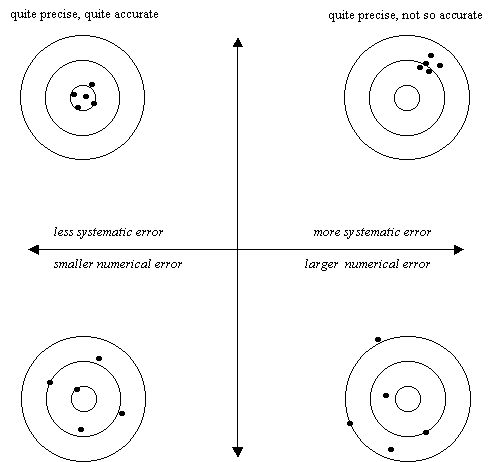
not so precise, quite accurate (if “averaged”)

not so precise, not so accurate

Significant Digits

Significant digits are the means by which scientists allow for uncertainty in numerical values. Significant digits are defined as those digits in a numerical value that are known with certainty and one additional digit that is uncertain. Significant digits do not affect error, but rather provide a way for us to acknowledge that error and uncertainty inescapably exists.

One of the main purposes of understanding and using significant digits is to allow us to communicate with others the approximate amount of uncertainty in a numerical result. Take for example the length of a table – if we report it as 123.4 cm then we are implying that the value is “good” out to the tenths place. Or put another way, even though we do not write it explicitly, we are implying that the length has approximate uncertainty of ± 0.1 cm.

It is important that you are able to identify the significant digits in numerical values. For example, if a length is given as 123.4 cm you should recognize that all of its digits are significant; the 1, 2, and 3 are the certain digits, and the 4 is the uncertain digit. Generally speaking the digit that is farthest to the right is the uncertain digit and all of the digits that precede it are taken to be certain. Zeros are sometimes an exception (and are a source of confusion when it comes to significant digits). Any zero that serves no purpose but to help “locate the decimal” or that is simply a “placeholder” is not a significant digit. Note that when scientific notation is used (numbers of the form M × 10ⁿ), every digit, zero or not, in the mantissa, M, is significant. The rest of the value – × 10ⁿ – locates the decimal and serves the same purpose as “placeholder” zeros and thus these are not significant digits.

A quantity written as . . .	Has these significant digits . . . (shown in bold italic)	And this approximate level of uncertainty . . .
356 m	356 m	± 1 m
1.9 s	1.9 s	± 0.1 s
2.006 L	2.006 L	± 0.001 L
70,005 kg	70,005 kg	± 1 kg
80.02 m	80.02 m	± 0.01 m
2.0 m	2.0 m	± 0.1 m
30.00 s	30.00 s	± 0.01 s
40.10 s	30.10 s	± 0.01 s
45.630 km	45.630 km	± 0.001 km
1.45 × 10^9 m	1.45 × 10^9 m	± 1 × 10^7 m
7.00 × 10^−7 s	7.00 × 10^−7 s	± 1 × 10^−9 s
0.84 g	0.84 g	± 0.01 g
0.0977 s	0.0977 s	± 0.001 s
0.00050 L	0.00050 L	± 0.00001 L
30 s	30 s	± 10 s
10,800 kg	10,800 kg	± 100 kg
3000 m	3000 m	± 100 m
3000 m	3000 m	± 10 m
3000 m	3000 m	± 1 m

Note that only the values that begin or end with “lots of zeros” have non-significant “placeholders”. Also note the proper usage of the underline in the last three examples.

Significant Digits in Calculations

Another important use of significant digits is estimating the approximate uncertainty in a calculated result. This is accomplished by using two “rules of thumb”: one for multiplication and division and the other for addition and subtraction. The same rule that is used for multiplication will also be used for all other functions in this class.

The rule of thumb for multiplication and division: the number of significant digits in a product or quotient is limited by the least number of significant digits found in the numbers being multiplied and/or divided. In this type of problem, count the number of significant digits in each given value and adjust the answer to the least number of significant digits. For this class we will use the same rule for other operations such as square root, sine, cosine, and tangent, logarithms, etc.

The rule of thumb for addition and subtraction: the number of significant digits in a sum or difference is limited by the smallest common significant decimal place of the numbers being added and/or subtracted. In this type of problem, look for the given value that has the greatest amount of uncertainty and then round your answer to the same decimal place. Note that in this case we are not counting the number of significant digits and it is possible for the number of significant digits to increase or decrease when using this rule.

For both rules it is usually the case that you will be rounding off your answer to a certain decimal place so that it does not have too many significant digits. However, in some cases you will need to “add some zeros” so that your answer has enough significant digits. Either way, by using these rules of thumb it is possible to express your answer with an appropriate amount of implied uncertainty. Note: for numerical calculations that involve multiple steps you should only round off the final answer – excessive rounding of intermediate calculations can have a significant effect on the value of the final answer. Never round off intermediate values to less than the number of significant digits that are found in the given information in a problem. It should be stated here that rounding and significant digits are not sources of error, if done properly. As stated previously significant digits are a way of being realistic and “honest” about the amount of error that truly exists in our work. It gives us a way of “keeping up with” the uncertainty in the numerical values we use.

Units of Measure

Almost all numerical values that we use in physics will have an associated unit or set of units. It is imperative that you include proper units on each and every numerical answer. In many problems it is necessary to convert units. It is also very helpful to use units as a means for checking and truly understanding your work. Being able to work with units in all of these aspects will make you a much better physics student.

SI and MKS

In this class we will primarily use units from the Système International (SI). These are also sometimes called “metric” units. In SI, the standards for length, mass, and time are the meter, the kilogram, and the second. Because these three units are so important it is sometimes referred to as the MKS system. These three base units are combined in various ways to produce other “derived” SI units such as the newton, the joule, the watt, etc. (Less commonly used is the CGS system, which is based on the centimeter, gram.)

Scientific Notation and Metric Prefixes

Because scientists study everything from the incredibly tiny (e.g. atoms) to the incredibly huge (e.g. galaxies) we must be able to cope with really small and really large numerical values. For example the wavelength of a He-Ne laser is about 0.000 000 633 m and the size of a typical galaxy is about 1 000 000 000 000 000 000 000 m in diameter. To make values such as these easier to comprehend and more convenient to write and read we use either scientific notation or a metric prefix.

“Scientific notation” refers to a value in the format M × 10ⁿ, where 1 ≤ M < 10 and n is an integer. For example the wavelength of a He-Ne laser is 6.33 × 10⁻⁷ m and the diameter of a galaxy is 1 × 10²¹ m. In order to be “proper” scientific notation the mantissa, M, must contain all of the significant digits in the value (and only those digits) and it must be greater than or equal to 1 and less than 10. For some numerical values (especially those that are difficult to determine with precision) the power of ten will be of the most interest to a scientist – the power of ten is sometimes referred to as the “order of magnitude”.

Metric prefixes serve essentially the same purpose as scientific notation and allow us to write the “power of ten” without having to literally write it as “ × 10ⁿ ”. Below are listed the most commonly used metric prefixes (which you are expected to memorize):

prefix	abbreviation	value	meaning
Giga-	G	10^9	billion
Mega-	M	10^6	million
kilo-	k	10^3	thousand
centi-	c	10^−2	hundredth
milli-	m	10^−3	thousandth
micro-	μ	10^−6	millionth
nano-	n	10^−9	billionth

This is not a complete list – other values can be found in your book or some other reference. Other prefixes you may have learned previously such as hecto-, deka-, and deci- are seldom used by scientists; centi- is primarily used just with the meter (as in centimeter) and is not often combined with other units. With this knowledge we can write our previously stated values as: wavelength of He-Ne laser = 633 nm and diameter of galaxy = 1 Zm (zettameter = 10²¹ m).

To “properly” use a metric prefix choose the one that will result in a value greater than 1 but less than 1000 as was done in the case of the wavelength. The same wavelength is equal to 0.633 μm or 0.000 633 mm or 6.33 × 10⁻¹⁰ km or 633000 pm (picometer = 10⁻¹² m), however using nanometers results in a value between 1 and 1000 and thus 633 nm is the preferred form. Generally speaking it is not desirable to combine scientific notation and a metric prefix in the same value. For example a length of 2.541 × 10⁸ mm should be written as either 2.541 × 10⁵ m or 254.1 km. There are some exceptions to this. Because the standard for mass is the kilogram, a value such as the mass of the earth is often written as 5.974 × 10²⁴ kg, but seldom will you see it written as 5974 Yg (yottagram = 10²⁴ g).

One final comment on this topic – unless there is a specific reason for using a certain prefix/unit combination, it doesn’t really matter which method is used to express very large or very small numbers – either scientific notation or an appropriate metric prefix is fine. However, neither method should be used for “ordinary” numerical values. For example, avoid writing values like 2.5 × 10² m or 3.0 × 10⁻¹ s when you can write 250 m or 0.30 s instead. Use a little common sense here – the goal is to write a numerical value in the manner that makes it easiest to comprehend.

Unit Conversions

It is often necessary to convert the units of measure in a problem. Most scientists use a technique known as the “factor label method” or “unit analysis”. To use this method one simply starts with some given numerical value and then multiplies it by a series of “conversion factors” to obtain the desired combination of units in the result. In order to do this correctly, there are two rules that must be followed: each multiplier has a numerator that is equivalent to its denominator and all units must “cancel” except for those that are desired in the final result. This is best understood by looking at a few examples.

Examples:

Convert 25 m/s into km/h

Convert 55 mph into m/s

Convert 206 m³ into L

Or, if you prefer, this can be written as:

You are expected to memorize these conversions:

1 L = 1000 cm³, 1 h = 60 min = 3600 s, 1 min = 60 s, 1 day = 24 h, 1 year ≈ 365 days.

The following conversions are also often useful (but you are not required to memorize):

1 inch = 2.54 cm, 1 ft = 12 in, 1 yard = 3 ft, 1 mile = 5280 ft ≈ 1609 m, 1 kg ≈ 2.205 lb(mass).

Except for those noted as approximations, all of the above conversions are exact and by definition have no uncertainty.