Graphical Analysis of Position, Velocity, and Acceleration

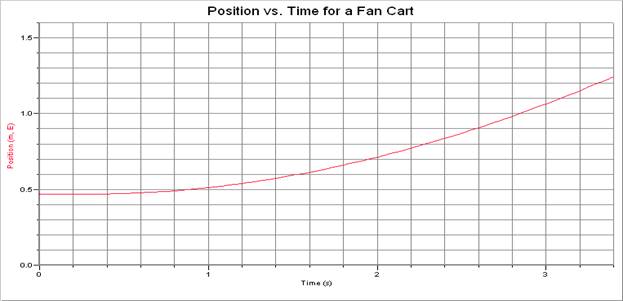
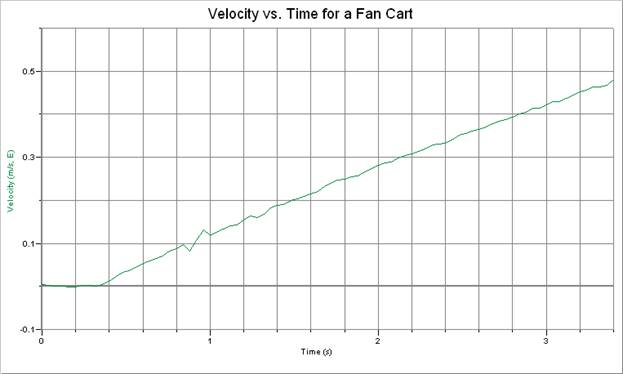
Both graphs describe the same event:  a fan cart released on a level track.

1. Using the velocity graph determine the cart’s average acceleration from 1.0 s to 3.0 s.

2. Would it be fair to say the cart had a constant acceleration?  If so, how is this apparent?

3. Determine the area under the curve on the velocity graph in order to find the displacement.

4. Use the position graph to find the displacement and compare to the previous result – it should be same.

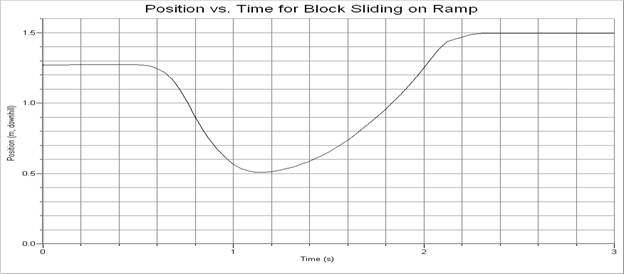
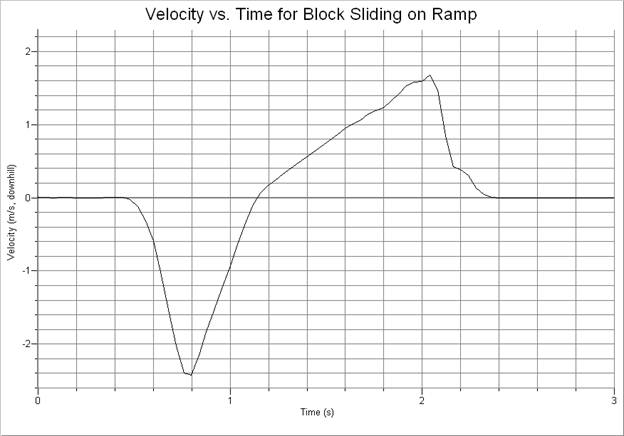
1. These graphs show a block pushed up a ramp, which then slides back down and is caught.  Identify the parts that are:  “the push”, “the slide up”, “the slide down”, and “the catch”.

2. (a) Determine the acceleration at 1.0 s and at 1.6 s by drawing a best fit line and finding the slope.  (b) Determine the acceleration at 0.5 s by using a tangent line.

3. (a) Identify the point in time at which the cart stops sliding up and begins sliding down. 
(b) Determine the acceleration at this point in time.

4. During what intervals of time is the block’s speed increasing? decreasing?

5. Find the maximum rate of acceleration.

6. Use each graph to find the block’s displacement and compare the two values.

Answers for Fan Cart:

1. a = 0.15 m/s², 0° (or 0.15 m/s², East)

2. Starting at about t = 0.4 s the data shows a fairly consistent linear pattern – however, on close inspection it appears to curve slightly downward.  Therefore we can say the acceleration is roughly constant and does not vary much, but it does appear that the acceleration decreases slightly as the speed increases.

3. ½ bh = ½ (3.05 s)(0.48 m/s) = 0.73 m, 0º

4. x_f – x_i = 1.24 m – 0.48 m = 0.76 m, 0º  The two values are essentially the same, allowing for error.

Answers for Block on Ramp:

1. On the velocity graph there are four diagonal sections – these are, in order: the push, the slide up, the slide down, and the catch.

2. a. at t = 1.0 s, a = 7.0 m/s², downhill; at t = 1.6 s, a = 1.8 m/s², downhill
b. at t = 0.5 s, a = 2.2 m/s², uphill

3. a. at t = 1.13 s the cart’s velocity is zero and it reverses its direction of travel (before this it is moving uphill, after this it is moving downhill).
b. a = 4.1 m/s², downhill

4. at t = 2.1 s, a = 16 m/s², uphill and 16 m/s² appears to be the maximum amount of acceleration (disregarding the direction of acceleration).

5. increasing speed:  0.45 s < t < 0.80 s and 1.13 s < t < 2.05 s  (the push and the slide down)
decreasing speed:  0.80 s < t < 1.13 s and 2.05 s < t < 2.40 s  (the slide up and the catch)

6. Using either the change in position on the first graph or area under the curve on the second graph the overall displacement is about 0.22 m, downhill.