AP Physics 1 Self Assessment Test Results
Use the table below to determine where to get help on the questions that you missed.
|
Question |
Topic |
Where to get help… |
|
1 – 5 |
Significant Digits |
Text (Giancoli) pp. 6 – 8 Mr. M’s World: Measurement Notes Mr. M’s World: Tutorials |
|
6 – 11 |
Accuracy, Precision, |
Mr. M’s World: Measurement Notes |
|
12 – 16 |
Unit Conversions |
Text (Giancoli) pp. 8 – 11 Mr. M’s World: Measurement Notes |
|
17 – 22 |
Graphical Analysis |
Mr. M’s World: Labs – Graphical Analysis |
Solution Key:
1. D. Only the last zero is a significant digit. The only reason to include the final zero is to indicate that the mass of the object is known to the nearest 0.0001 kg. (i.e. There is significance to writing 0.0040 kg instead of 0.004 kg.) The leading zeros are sometimes described as “placeholders”, the only purpose of which is to “locate the decimal”. These are not “significant” as they are unnecessary if the mass is written in other ways such as 4.0 g or 4.0 × 10−3 kg.
2. B. ±1 m/s. The general concept of significant digits is to include those known with certainty and one digit (the “final” one) that contains uncertainty. If the last digit is uncertain, then the value 343 m/s has uncertainty on the order of 1 m/s.
3. C. 17.6 m. A sum or difference can only be as precise as the least precise addend. In this case both addends are equally precise, with uncertainty in the tenths place. Therefore the resulting sum is also uncertain in the tenths place. Notice the rule for counting the number of significant digits does not apply to this problem.
4. B. 64 m2. When multiplying or dividing the number of significant digits in the result is limited to the multiplicand with the least number of significant digits.
5. C. 5.00 m/s. Both given values have three significant digits, as does the resulting quotient. Note: all of the zeros in this problem are significant.
6. B. Team B is more precise than Team A. Less deviation in results indicates better repeatability and higher precision. This has nothing to do with the true value for the expansion rate of the universe.
7. D. It cannot be determined which is more accurate without knowing the true expansion rate. It is possible that 75 km/s/Mpc is closer to the true value and if this is the case it would be the most accurate. Note: The deviation values given are based on differences noted when repeating the experiment and have nothing to do with the true value.
8. A. This is systematic error that will affect accuracy but not precision. Because of the problem with the ruler, all of the student’s measurements will be greater than the true length (by about 0.1 cm each time). However, the consistency and repeatability of the measurements will not be affected.
9. B.
27%
![]()
10. A. 1.5 μm.
Deviation is the difference between one value of a set and the mean of that
set. The mean of this set is 86.0 μm and the absolute values of the
deviations in the set are 2.4, 0.1, 0.3, 1.7, 3.5, 1.0 μm. The correct
answer is the mean of this set of deviations. Note this is not the same thing
as “standard deviation”.
11. C. Random error has an unpredictable effect on data and causes scattering of values. This is a different use of the word random than in the expression “random act of violence”. Random error causes measurements to be both too high and too low, without “preference” to one or the other.
12. D. 1.5 × 1011 m.
150 Gm = 150 gigameters = 150 ´ 109
m = 1.5 × 1011 m.
13. C. 32 μm.
3.2 × 10−5 m = 32 × 10−6 m = 32 micrometers =
32 μm.
14. A. 8.29 mi/s
![]()
15. D. 4680 in2
![]()
16. C. 84 kg/m2
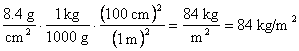
17. A. Temperature is the independent variable and belongs on the x-axis. The volume depends on the temperature, not the other way around.
18. D. The line should pass “through the center” of the data, with points scattered equally above and below the line. This allows for random error in the data.
19. C. The line of best fit shows the most likely actual relation between the x and y variables.
20. B. It does not support the 2nd Law because the data is clearly not linear. If force and acceleration were directly proportional to one another the graph should be linear, not curved.
21. B. y = ax2 + bx + c The data forms what appears to be a parabolic curve.
22. A. The data is quite precise but there is significant systematic error. Because the data points are all fairly close to the parabolic curve the data may be described as highly precise (i.e. consistent). Only a systematic error would cause data to curve in a particular direction and fail to be linear.