Periodic Motion Lab – The Conical Pendulum

 

Purpose

The goals of this lab are to verify that centripetal acceleration is given by a = v2/r and to show that the period of a conical pendulum is given by the theoretical equation: 

 

Procedure

A small mass is suspended by a cord and set into motion above a “target” circle.  It then moves in a horizontal circle under the influence of gravity and the tension in the cord.  As it moves, the mass and string trace out an imaginary cone – hence it is referred to as a conical pendulum.  The radius, r, and length, l, are measured with a ruler or meter stick.  Both r and l should be measured to the center of the mass.  The period, T, is measured using a stopwatch.  It is best to time a certain number of revolutions and divide by this number to get the period.  All other values are calculated based on these three measurements.  The “height” h will not be measured directly.

 

 

 

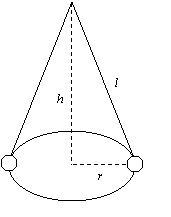
Part I – Centripetal Acceleration

Vary the value of r and measure the value of T while keeping the ratio of l to r constant.  Use a ratio of l/r = 7.  (By keeping this ratio constant, the centripetal acceleration will theoretically remain constant according to Newton’s Laws.)  In order to achieve this, you must measure the radius of one of the circles and then adjust the length to seven times this amount (we could have used any ratio, but seven is a convenient value using this equipment).  Once a trial is complete, choose another radius and readjust the length and repeat.

 

Part II – Period dependence on h

Vary the value of l and measure the value of T while keeping r constant. Choose one of the “midrange” circles and use the same one each time while changing the length of the string from trial to trial.  Record the value of this radius.  Then choose six lengths that will cause a significant change and cover as wide a range of periods as possible.

 

Analyses

 

1.      Complete the tables by calculating speed, speed squared, and acceleration for Part I, and by calculating the height h and the constant k for Part II.

2.      Produce a graph for Part I showing speed squared vs. radius.  Determine the line of best fit and corresponding equation.

3.      Produce a graph for Part II showing period vs. height.  This should be a curve of the form:  .  Use the mean value for k and write this equation in finalized form on the graph.  Then plot this equation and connect with a smooth curve for comparison with the data points.

 

Questions

 

1.      (a) Make a free body diagram of the pendulum mass as it moved in its circular path. 
(b) What force or what component of force is the centripetal force for the mass?

2.      (a) Use F = ma to solve for the centripetal acceleration of the mass in Part I.  Show your work.  Hint:  the mass will not affect the result, but the result is affected by the amount of tilt in the string (which relates to the ratio of l/r).
(b) Explain why the acceleration should be constant as long as the ratio of length to radius does not change.

3.      Taking the theoretical value of acceleration found in the previous question as the accepted value:  (a) Calculate the percent error in the mean value of the calculated acceleration found in the table.  (b) Calculate the percent error in the slope of the graph.

4.      (a) Use the mean value of k to determine the value of g.  (Hint: the theoretical equation should equate with the curve fit equation.)  (b) Calculate the percent error in this value for g.

5.      The theoretical equation for period in this experiment is very similar to simple harmonic motion equations for period.  If the mass in this experiment had been swung like a normal pendulum (moving back and forth in one plane) would it have had the same period as the conical pendulum (moving in a horizontal circle)?  Discuss and explain.

6.      Discuss Error.  As always, this means to evaluate imperfections in the results.  Make specific references to evidence of error and the most probable sources of error responsible for these unexpected results.

 

 

A complete report (50 pts):  (5 or 6 pages in this order)

q       Completed data/observations tables.  (10)

q       Speed Squared vs. Radius graph w/ line of best fit and equation.  (14)

q       Period vs. Height graph w/ curve of best fit and equation.  (14)

q       On separate paper, answers to the questions using complete sentences.  (12)

Data/Observations

 

 

Part I – Centripetal Acceleration

 

Measured Values

Calculated Values

Radius
(m)

Length
(m)

Period
(s)

Speed
(m/s)

Speed2 (m2/s2)

Acceleration (m/s2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Mean Acc:

 

 

 

 

 

Part II – Period of Conical Pendulum

 

Radius =                                                             (Same for all trials)

Measured Values

Calculated Values

Length (m)

Period (s)

Height (m)

(s m-1/2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Mean k:

 

 

 

 

 

Target Circle

 
Suspend the mass over this pattern and twirl it until it “hovers” over one of the circles with its center tracing the path of the circumference.