Simple Harmonic Motion – Overview
In order for simple harmonic motion to occur, the following condition must be true:
![]() and
and ![]()
where: F = net force acting on an object
k = a constant (a positive value in the above equation)
x = position of the object
m = mass of the object
a = acceleration of the object
If such an object is set into motion it will oscillate about its point of equilibrium and its position, velocity, and acceleration will be described by the following:
![]()
![]()
![]()
where: A = amplitude of the oscillation (maximum displacement from equilibrium)
ω = angular frequency
t = time
f = phase angle
Furthermore the angular frequency and period of the oscillation are governed by the following:
![]()
![]()
Some important points concerning this motion:
The maximum speed of the object is given by Aω and this occurs at x = 0.
The maximum acceleration rate of the object is given by Aω2 and this occurs at x = ± A.
It can be shown that a very close approximation of simple harmonic motion occurs about any point of stable equilibrium so long as the amplitude of oscillation is small. In such a case the constant −k is determined by the slope (derivative) of force versus position at the point of equilibrium.
The following graphs illustrate an object undergoing simple harmonic motion assuming the phase angle is zero.
Note that the time is given in multiples of the period, T, the position is given in multiples of the amplitude, A, the velocity is given in multiples of the maximum speed, Aω, and the acceleration is given in multiples of the maximum rate of acceleration, Aω2.
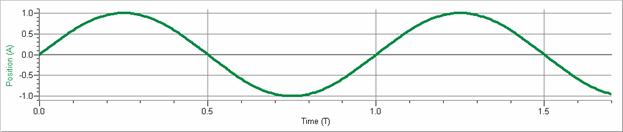

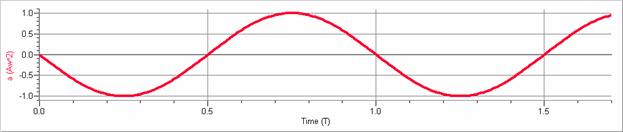
Note the pattern:
|
t |
0 |
0.25T |
0.5T |
0.75T |
1.0T |
1.25T |
1.5T |
|
x |
0 |
A |
0 |
−A |
0 |
A |
0 |
|
v |
Aω |
0 |
− Aω |
0 |
Aω |
0 |
− Aω |
|
a |
0 |
− Aω2 |
0 |
Aω2 |
0 |
− Aω2 |
0 |
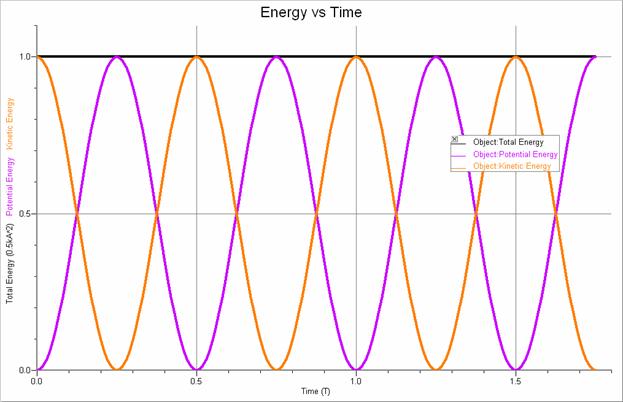
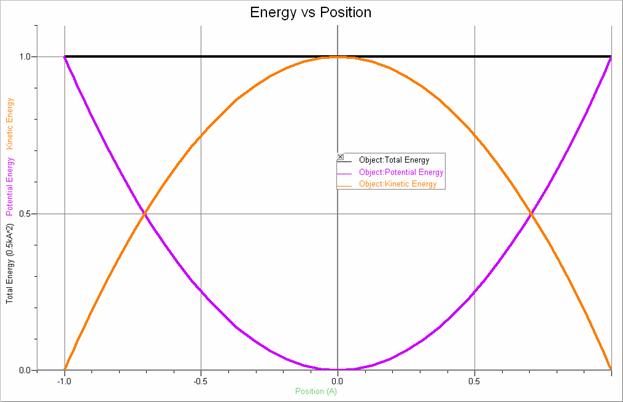
Shown below are additional graphs that illustrate the energy of an object undergoing simple harmonic motion. It can be shown that the total energy of such an object is given by E = ½ kA2.
Note that the time is given in multiples of the period, T, the position is given in multiples of
the amplitude, A,
and the energy is given in multiples of the total energy, ½ kA2.