AP Physics Rotational Mechanics Lab
The purpose of this investigation is to verify various relations of rotational motion including torque, moment of inertia, conservation of angular momentum, etc. This will be accomplished using a rotary motion sensor connected via Lab Pro Interface to a laptop computer. The program Logger Pro 3 will interpret data from the sensor and produce graphs of angular position, angular velocity, and angular acceleration.
Procedure
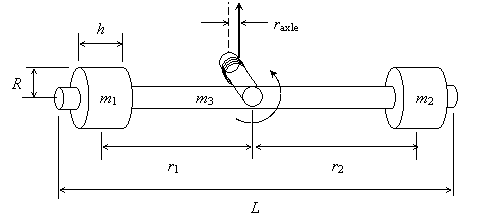
Attach the rotary motion sensor to a ring stand so that the axis of rotation is horizontal as shown in the diagram. The larger diameter of the pulley should face outward. Attach the thin rod to the pulley – note the notches on the pulley that prevent the rod from slipping as the pulley rotates. Attach the two brass “collars” to the ends of the rod. Adjust the position if necessary so that the rod and collars are balanced about the axis of rotation (rod will remain stationary in any position).

Part A – Torque, Moment of Inertia, Angular Acceleration
1. Connect the LabPro interface to a USB port and plug in its power supply to a wall outlet.
2. Connect the Rotary motion sensor to DIG/SONIC 1.
3. Run the Logger Pro program with the file: AP Rotation. A message may appear concerning the sensors – click OK. You may use the Save As command to save your data in a file with the last name of one of the persons in your group. Feel free to Save as often as you like so that you could easily recover a previous step if you make mistakes.
4. Give the rod a spin and allow it to rotate freely. Then use Logger Pro to collect data showing the angular deceleration. Find the angular acceleration by linear regression of angular velocity vs. time. Record the results in the table in the row that shows zero applied torque. This is a measure of the effect of friction within the sensor.
5. Use a very small piece of “Scotch” tape to attach the free end of the thin string to the axle on the side of the sensor opposite of the rod and masses. Carefully turn the axle and wind the string around the axle in a single layer – do not let the string wrap on top of itself.
6. Determine the radius of the axle indirectly by measuring how much string is added or removed to the windings on the axle for a given number of revolutions of the rod. For example you might turn the rod precisely 4 times and use a meter stick to observe that a certain number of centimeters of string has unwound. This information can be used to determine the effective radius of the axle by using the relation: s = rθ.
7. Now attach the spring scale to the end of the string and pull upward with a constant force of 0.50 N – this will cause the rod to accelerate, which can be measured with Logger Pro. Note: it is not necessary to pull the string completely off of the axle – the lab will go quicker if you keep some amount of string wound on the axle.
8. Repeat the process at forces of 1.0 N, 1.5 N, and so on until the table is completed.
9. Remove the string, tape, and rod from the pulley. Measure the dimensions and masses of the rod and brass collars. Record this information in the table.
Part B – Atwood’s Machine
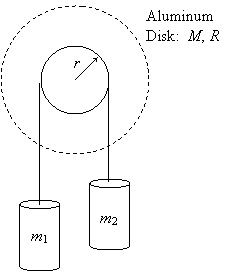
10. Reverse the pulley and secure it to the axle so that the larger diameter groove is facing the sensor. Pass a string over the pulley in the groove with the largest diameter. Hang 100.0 g of mass on one end of the string and 90.0 g on the other.
11. Give the lighter mass a gentle pull downward and release it so that it travels downward a ways before it reverses and rises under the influence of the heavier mass on the other end. Use Logger Pro to produce graphs of this motion. Use a curve fit or linear regression to determine the angular acceleration as lighter mass falls and as lighter mass rises. Print a copy of the angular velocity vs. time graph showing the two linear regressions.
12. Measure the mass and radius of the aluminum disk.
13. Attach the aluminum disk to the pulley and repeat the experiment. Once again print a copy of the graph to include in your report.
Part C – Conservation of Angular Momentum
14. Remove the sensor from the ring stand and reattach it so that the axis of rotation is now vertical and the aluminum disk is horizontal on the top side of the sensor. In this part of the lab you will spin the disk and gently drop objects on top of it and measure the resulting decrease in its angular speed.
15. Conduct a series of experiments in which you start the disk spinning and then gently drop an object on top of it. Be careful to not contact the object that you drop after it hits the disk. Record in the table a description of the second object, including its dimensions and mass. Note: you can use the black ring in two ways – it can be dropped onto the rotating aluminum disk or it can be attached to the disk (note the two “pegs”) and included as part of the initial angular momentum before dropping an object on top of it (instead of the disk).
Analyses
1. Construct a graph of Applied Torque vs. Angular Acceleration using the data from Part A. Determine the line of best fit.
2. Show work on a separate piece of paper and include in your report: (a) Calculate a theoretical angular acceleration for the Atwood’s machine based on the two masses and the assumption of massless and frictionless pulley. (b) Calculate a theoretical angular acceleration for the Atwood’s machine with aluminum disk attached (but still assuming no friction).
3. Determine the percent change in the angular momentum for each trial of Part C and include in the table.
Part A – Torque vs. Angular Acceleration
|
ra = |
Show all work used to determine ra and I: |
|
|
h = |
||
|
R = |
|
|
|
m1 = |
|
|
|
m2 = |
|
|
|
r1 = |
|
|
|
r2 = |
|
|
|
m3 = |
Total Moment of Inertia |
|
|
L = |
I = |
|
|
String wrapped around axle of pulley: |
Regression of Angular Velocity vs. Time: |
||
|
Force |
Torque = raF |
Angular Acceleration (rad/s2) |
Correlation Coefficient (no units) |
|
0.0 |
|
|
|
|
0.5 |
|
|
|
|
1.0 |
|
|
|
|
1.5 |
|
|
|
|
2.0 |
|
|
|
|
2.5 |
|
|
|
Part B – Atwood’s Machine
|
r = 2.385 cm |
|
m1 = |
|
m2 = |
|
M = |
|
R = |
|
|
α1 (rad/s2) lighter mass falling |
α2 (rad/s2) lighter mass rising |
|
Pulley Alone |
|
|
|
Pulley and Aluminum Disk |
|
|
Part C – Conservation of Angular Momentum
|
|
Before |
After |
|
||||
|
|
I1
|
ω1
|
L1
|
I2
|
ω2
|
L2
|
% change in L |
|
Trial 1 |
|
|
|
|
|
|
|
|
Trial 2 |
|
|
|
|
|
|
|
|
Trial 3 |
|
|
|
|
|
|
|
|
Trial 4 |
|
|
|
|
|
|
|
Questions
1. (a) What does the slope of torque vs. angular acceleration represent? (What should it equal?) (b) Calculate the percent error in the slope.
2. Discuss whether or not and how well or not the graph of torque vs. angular acceleration supports the concepts of rotational dynamics. Incorporate some discussion of error. Be specific.
3. Discuss the results of the Atwood’s Machine experiment. Compare the theoretical values of angular acceleration with the measured values and discuss error. Be specific. (An advanced analysis of your results would allow you to determine the internal frictional torque of the sensor and the moment of inertia of the pulley (not including the disk).)
4. Discuss the results of the experiments concerning conservation of angular momentum. Discuss error. Be specific.
A complete report (50 pts): (pages in this order)
q Data Tables (8)
q Torque vs. Angular Accleration graph, with regression equation. (8)
q Angular Velocity vs. Time for Atwood’s Machine, with two regression equations. (8)
q Angular Velocity vs. Time for Atwood’s Machine with Aluminum Disk attached, also showing two regression equations. (8)
q Page of calculations of theoretical angular acceleration of the Atwood’s experiments. (8)
q On separate paper, responses to the questions. (10)