AP Physics Assignment - Induction and Inductance

AP Physics Assignment – Induction and Inductance

Reading Chapters 31 and 32, pp. 952 – 956

Objectives/HW

	The student will be able to:	HW:
1	State and apply Faraday’s Law and Lenz’s Law and solve magnetic induction problems involving changing magnetic flux, and induced emf or eddy currents.	1 – 16
2	Solve problems involving basic principles of generators, including production of back emf.	17 – 21
3	State and recognize Maxwell’s equations and associate each equation with its implications.	22 – 23
4	Define and calculate inductance and solve related problems including those that involve parallel or series inductors.	24 – 31
5	Analyze RL circuits in terms of the appropriate differential equation and resulting exponential functions for charge, current, voltage, etc.	32 – 38
6	Analyze LC and RLC circuits in terms of the appropriate differential equation and resulting exponential functions for charge, current, voltage, etc.	39 – 41

Homework Problems

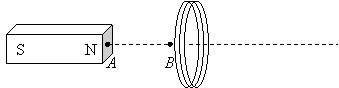
1. A permanent bar magnet is located near a circular coil of wire and moves along the axis of the coil as shown in the diagram below. For each of the following events describe the direction of the current induced in the coil. Let a “positive” current mean that current at the top of the coil goes into the page (i.e. the sense of the emf is leftward by the right hand rule). (a) The magnet moves from point A to point B. (b) A force is applied to each side of the coil until it “collapses” into an ellipse with less area than its original circular shape (while magnet remains stationary). (c) The magnet is rotated 90° about its North pole.

2. The square loop of wire in the diagram moves through equally spaced points A through E at a constant velocity. Point C is located at the midpoint between the poles of a horseshoe magnet. (a) Carefully sketch a graph of magnetic flux vs. time for the square loop and label points A through E. (b) Carefully sketch a graph of current vs. time for the square loop and label points A through E. Let positive values represent counterclockwise current in the loop.

3. A circular loop of wire in the xy-plane is near a current along the x-axis as shown below. For each of the following events describe the magnetic flux as increasing, decreasing, or constant and describe the induced current in the loop as clockwise, counterclockwise, or zero. (a) The current increases. (b) The loop is moved in the positive x-direction. (c) The loop is moved in the positive y-direction. (d) The wire is moved in the positive y-direction. (e) The loop is bent and reshaped into an ellipse. (f) The loop is rotated 30° about an axis through its center that is parallel to the y-axis. (g) The loop is rotated 30° about the x-axis.

4. A uniform magnetic field points in the positive z-direction. A wire loop in the shape of a circle with diameter 25.0 cm lies in the xy-plane. The total resistance of the wire is 33 mΩ. Suppose the magnitude of the magnetic field increases at a constant rate from 0.10 T to 0.30 T in 4.0 s. (a) Find the initial magnetic flux for the loop. (b) Find the emf induced in the wire. (c) Find the current in the wire.

5. A single square loop of wire with sides of 5.00 cm is placed in the xy-plane. A uniform magnetic field points in the positive z-direction and has a magnitude that varies as shown in the graph below. (a) Find the induced emf at t = 0.050 s. (b) Find the induced emf at t = 0.15 s. (c) Find the induced emf at t = 0.22 s. (d) Find the induced emf at t = 0.27 s.

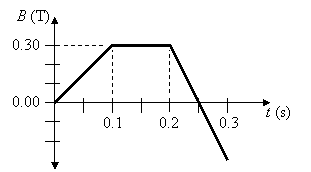
6. Suppose the scenario above is repeated with one exception – the width of the square is doubled. (a) What would be the effect on the results? Explain. (b) How would the current induced in the two coils compare? Explain.

7. The magnetic field perpendicular to the plane of a single copper wire loop of diameter 20.0 cm decreases from 0.60 T to zero. The diameter of the wire is 1.30 mm. How much charge moves through the wire as a result of the changing field?

8. A long cylindrical solenoid with radius 2.00 cm and 650 turns per meter is connected to a power supply and the current through it is increased at a constant rate from 0 to 8.00 A in 0.25 s. (a) Sketch a cross-section of the solenoid and the induced electric field that occurs. (b) Find the magnitude of the electric field at r = 1.00 cm from the axis. (c) At what other location(s) would the electric field have the same magnitude as at r = 1.00 cm? (d) The induced electric field does what work on a single electron as it completes a single turn of the wire?

9. Suppose a cylindrical solenoid of radius R and turns per length n has a clockwise current that decreases according to the function I = I₀e^-^kt. Derive expressions for the induced electric field as a function of r, the radial distance from the axis.

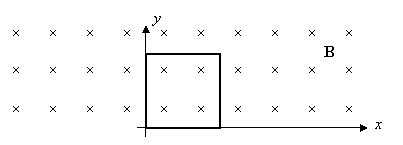
10. The diagram below shows a loop of wire with total resistance R and sides of length L. The loop is located in a uniform magnetic field of magnitude B that is confined to the first and second quadrants (drops to zero in other quadrants). (a) Determine an expression for the current induced in the wire if the loop moves downward with constant speed v. (b) Find the amount of force that must be applied to the loop in order to move it thusly. (c) Find the energy dissipated by the electric current and show that is equals the work done to remove the loop from the field.

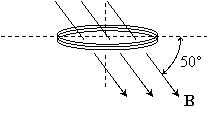
11. The figure below depicts a circular loop of wire with 330 turns, radius 15.0 cm, and resistance 4.00 Ω held in a horizontal plane. Also shown is the Earth’s magnetic field which points north and down at an angle of 50.0° and has magnitude 55 μT. (a) Find the initial magnetic flux for a single turn of the coil. The coil is now rotated 50.0 ° so that the flux drops to zero. (b) In what direction does current flow? (c) In order to produce a measurable current that averages 10.0 μA, the repositioning of the loop must occur in what amount of time?

12. At a certain location the Earth’s magnetic field has magnitude 0.50 G and points precisely horizontal and North. A car with a vertical antenna of length 80.0 cm travels at 25.0 m/s on a level roadway. (a) In what direction should the car travel if the induced emf in the antenna is to be maximized and positive at the top? (b) What is the maximum induced emf? (c) Repeat, but this time with the antenna tilted at 30.0 ° relative to horizontal.

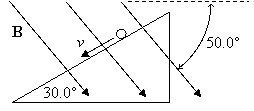
13. A long metal bar at a construction site rolls southward and down an incline of 30.0° in a region where the Earth’s magnetic field is 0.60 G north and down at an angle of 50.0° relative to horizontal. If bar reaches a speed of 10.0 m/s and has a length of 4.0 m, what is the induced potential difference between its ends? Which end is “positive”?

14. A metallic bar moves along frictionless metallic rails at a constant speed of v = 5.0 m/s as shown in the diagram below. The rails are connected to a resistor of 3.0 Ω. The entire circuit is in a uniform magnetic field of 0.40 T. (a) Find the resulting current in the circuit. (b) Determine the applied force necessary to move the bar in such a fashion. (c) Find the rate at which mechanical work is done in moving the bar. (d) Find the power dissipated by the resistor.

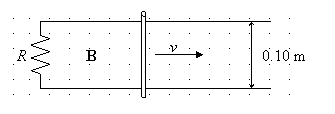
15. A straight piece of wire is moved along a U-shaped piece of wire in a uniform magnetic field of 0.75 T as shown below. All of the wire has resistance per unit length equal to 0.25 Ω/m and the straight wire moves at constant speed 4.0 m/s to the left. Find the current when: (a) x = 7.0 cm and (b) x = 2.0 cm.

16. A square loop of wire with sides of length 5.00 cm moves at 10.0 m/s away from a long wire with current 20.0 A. The square and the wire are in the same plane. For the instant when the center of the square is 10.0 cm from the wire determine: (a) the magnetic flux through the loop and (b) the induced emf.

17. A simple generator consists of a rectangular coil of 100 turns and dimensions 10.0 cm × 5.00 cm that rotates in a uniform magnetic field of 125 mT. The coil rotates at a steady 2340 rpm. (a) Find the maximum emf induced in the coil as it turns at this rate. (b) If the generator is connected to a 3.0 kΩ resistor what is the maximum power output (ignore resistance of the coil)? (c) Using the same resistor, what rotation rate would be necessary to double the power output?

18. A certain generator is connected to a 1.2 kΩ resistor. The current through the resistor peaks at 5.00 mA and reverses direction every 33 milliseconds. The coil inside the generator is a square loop of sides 2.0 cm and negligible resistance turning in a uniform magnetic field of 0.400 T. (a) What is the angular frequency of the rotating coil? (b) How many turns are on the coil? (c) How much does the coil rotate as the current drops from 5.00 mA to 2.50 mA and how much time does this take?

19. Suppose an electric drill is drilling a hole in a piece of wood. If the operator pushes harder on the drill, the electric motor slows down. (a) What is the effect on the current drawn by the electric motor? Explain. (b) What is the effect on the torque due to magnetic forces inside the motor? Explain.

20. A simple motor is powered by a 5.00 V source and consists of a coil rotating in a uniform magnetic field. It is observed that the current in the motor decreases from 165 mA to 45.0 mA as the rotation rate goes from zero to a steady 125 rpm. Determine the back emf as the motor turns at 125 rpm.

21. Imagine a DC electric motor which is completely frictionless and operating in a vacuum. If connected to a power supply of a given voltage would the motor attain a constant angular velocity? Or would it undergo angular acceleration indefinitely? Explain.

22. Explain how Maxwell’s modification to Ampere’s Law (the addition of the “displacement current”) is necessary to explain the existence of electromagnetic waves in which electric and magnetic fields oscillate.

23. If Maxwell’s equations are said to summarize all electrical and magnetic phenomena what happened to Coulomb’s Law (the inverse square law governing attraction and repulsion of charges)? Why is it not a necessary part of Maxwell’s equations?

24. An inductor is any coil or loop of wire and may be described as a “moderator” of current. Explain this by answering the following questions: (a) If there is a current through the loop, why must there be magnetic flux through the same loop? (b) If the current increases, why must the magnetic flux also increase? (c) According to Lenz’s Law an emf is induced in what direction or sense relative to the current? (d) Why would this have a moderating effect? (e) What happens if the current decreases?

25. (a) If can be said that any and every electrical circuit has a certain amount of inductance – explain. (b) Having said that, unless there is a multiple-turn coil in the circuit the amount of inductance will be negligible – explain.

26. An inductor of 12 mH of negligible resistance is arranged vertically and the current through it is controlled by a variable power supply. Taking a positive value to mean that the top of the inductor is “positive”, find the emf in each of the following cases: (a) Current is 2.0 A upward and constant. (b) Current is 2.0 A upward and decreasing at 5.0 A/s. (c) Current is 5.0 A downward and increasing at 2.0 A/s. (d) Current is 0.100 A downward and decreasing at 2.0 A/s.

27. A certain inductor consists of a coil of wire that has a resistance of 5.0 W and an inductance of 2.0 mH. A current of 20.0 mA passes to the right through the inductor. Find the potential difference of the right side of the inductor relative to the left side should one of the following occur: (a) The current remains constant. (b) The current increases at 20.0 A/s. (c) The current decreases at 5.0 A/s.

28. A student uses a computer to measure the current and emf for a coil of wire of negligible resistance. It is found that the emf of the coil is 35 mV as the current increases from 155 mA to 195 mA in 0.0100 seconds. What is the inductance of the coil?

29. Show that inductance may be defined as magnetic flux per current by setting the emf of an inductor equal to Faraday’s Law and solving for the inductance.

30. An inductor is made by wrapping wire around a wooden dowel of length 15.0 cm and diameter 2.00 cm. If wrapped as tightly as possible, the wire forms 45 turns per centimeter. (a) Determine the inductance if one layer of wire is wrapped tightly from end to end. (b) In order to achieve a higher inductance, multiple layers of wire can be wrapped. How many total turns would be required to achieve 5.0 mH?

31. A certain square coil of wire consists of 100 turns and has an inductance of 2.0 mH. Find the inductance of (a) a square coil with the same number of turns but twice the area, (b) a coil with the same area but with 200 turns.

32. The current through a 0.30 mH inductor varies according to I = 2 cos(380t), where I is in amperes and t is in seconds. (a) Find the emf of the inductor at t = 0.10 s. (b) What is the maximum emf? (c) All other parameters being the same, what angular frequency of the current would be required to yield a maximum emf of 0.50 volt?

33. In the circuit shown below the switch is closed at t = 0 and then reopened at t = 10.0 s. (a) Find the voltage and current of the inductor at t = 0. (b) Find the voltage and current of the inductor at t = 10.0 s. (c) Sketch graphs of voltage vs. time and current vs. time for the inductor. (d) If the inductor is 10.0 mH, what is the rate of change in its current at t = 0 and at t = 10.0 s? (e) Which of your answers, if any, would change with a different inductor?

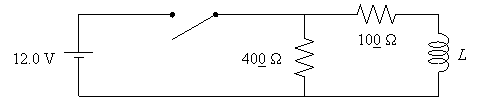
34. Examine the circuit shown below in which the switch has been in the closed position. (a) Find the current and voltage of the inductor immediately after the switch is opened. The switch remains open for a long time. (b) Find the current and voltage of the inductor immediately after the switch is closed again.

35. The switch in the circuit shown below is closed at t = 0 and then reopened at t = 10.0 s. (a) Find the voltage across each inductor at t = 0. (b) Find the rate of change in the voltage across R₂ at t = 0. (c) Find the voltage across each inductor at t = 10.0 s. (d) Find the rate of change in the voltage across R₂ at t = 10.0 s. (e) Produce a detailed sketch of the graph voltage vs. time for the inductor L₁.

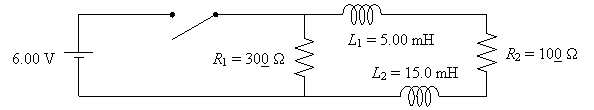
36. A slinky with 175 turns, radius 3.50 cm, and resistance 8.0 Ω is stretched to a length of 90.0 cm. A battery with emf 5.70 V and internal resistance 2.0 W is connected to establish a current through the slinky. (a) What will be the maximum current through the slinky if it stays connected to the battery? (b) How much time will it take for the current to go from zero to 90.0% of its maximum? (c) What is the emf of the slinky and what is the voltage across it at that same point in time?

37. An inductor of 75 mH and negligible resistance is “discharging” through a resistor of 550 Ω (the two devices are connected in a simple series loop). The current at t = 0 is 20.0 mA. (a) Find the initial voltage across the inductor. (b) Find the initial rate of change in the current. (c) Find the current and voltage at t = 0.100 ms. (d) Find the total heat dissipated by the resistor as the current drops to zero. (e) A capacitor of what capacitance and what initial charge would discharge identically if connected to the same resistor?

38. In the circuit shown below the emf = 12.0 V, L = 44 mH, and R = 50.0 Ω. (a) Find the change in the steady state current through the battery when the switch is moved from open to closed. (b) How much time does it take for 99.0% of this change to occur? (c) How much time does it take for 99.0% of the change to occur when the switch is reopened? (d) Make a careful sketch of the voltage vs. time graph for the inductor, including appropriate numerical values.

39. A capacitor of 2200 μF is charged to 6.0 V by a battery. Then it is removed from the battery and at t = 0 it is connected to an inductor of 11 mH. Ignore resistance. (a) With what frequency will the voltage of the capacitor oscillate? (b) What is the maximum current and at what value of t does it first occur? (c) How much energy is in the system? (d) At what voltage and current is the energy equally split between that of the capacitor and that of the inductor?

40. A certain Tesla coil has a solenoid of diameter 8.0 cm, length 30.0 cm, and 660 turns of wire. Attached to one end of the wire atop the solenoid is a metal sphere of diameter 20.0 cm. The other end of the wire leads to ground (earth). This forms in essence an LC circuit in which the L is the solenoid and the C is the isolated sphere (in conjunction with the Earth which can be taken as “infinity”). When in operation, a high frequency current passes back and forth through the solenoid as the sphere takes on charge of opposite sign at the same frequency. Ignore resistance. (a) Find the frequency of the oscillations in current and charge. (b) If the maximum voltage of the sphere is 110 kV, how much energy is present? (c) What is the maximum current? (d) A separate LC circuit with the same frequency is used to “excite” the solenoid and sphere. If this circuit has an inductor of 12 μH, what must be the value of the capacitor?

41. In an oscillating LC circuit, the maximum charge on the capacitor is 2.0 μC and the maximum current through the inductor is 6.0 mA. (a) Determine the frequency of the oscillations. (b) If the maximum voltage is 0.30 V, what are the values of L and C?