AP Physics Assignment – Magnetostatics
Reading Chapters 29 and 30
Objectives/HW
|
|
The student will be able to: |
HW: |
|
1 |
Define and illustrate the basic properties of magnetic fields and permanent magnets: field lines, north and south poles, magnetic compasses, Earth’s magnetic field. |
1 – 2 |
|
2 |
Solve problems relating magnetic force to the motion of a charged particle through a magnetic field, such as that found in a mass spectrometer. |
3 – 10 |
|
3 |
Solve problems involving forces on a current carrying wire in a magnetic field and torque on a current carrying loop of wire in a magnetic field, such as that found in a motor. |
11 – 18 |
|
4 |
State and apply the Biot-Savart Law and solve such problems that relate a magnetic field to the current that produced it. |
19 – 24 |
|
5 |
State and apply Ampere’s Law and Gauss’s Law for magnetic fields and solve related problems such as those involving parallel wires, solenoids, and toroids. |
25 – 39 |
|
6 |
Qualitativey describe and model behavior of magnetic materials using concepts of domains, ferromagnetism, paramagnetism, and diamagnetism. |
40 – 44 |
Homework Problems
1. An iron nail is rubbed against a magnet and becomes magnetized in the process. The nail is hung by a long thread and allowed to rotate about its center. It is found that the sharp end of the nail points geographically southward. (a) Which end of the magnetic nail is the north pole? (b) A magnetic compass brought close to the nail would point toward which end of the magnetic nail? (c) Make a sketch of the nail showing its poles and the magnetic field that it produces.
2. Suppose two identical bar magnets are laid side by side and parallel to one another a few centimeters apart on a table. Sketch the field in the plane of the table for each case: (a) the north poles face the same direction and (b) the north poles face opposite directions. Hint: use the superposition principle and also imagine which way a compass would point.
3. A uniform magnetic field of 0.250 mT points horizontally eastward in a certain volume of space. A particle with charge 50.0 nC is located in this volume. Determine the magnetic force on this particle if it moves with velocity: (a) 10.0 m/s vertically upward, (b) 20.0 m/s horizontally northward, (c) 20.0 m/s horizontally 30.0 ° north of east, (d) 30.0 m/s horizontally westward.
4. Derive a formula for the frequency with which a charged particle moves in a circular path when traveling in a plane perpendicular to a uniform magnetic field.
5. Consider the effect of a magnetic field on a charged particle. (a) In what circumstances, if any, does a magnetic field increase the speed of a charged particle. Explain. (b) Explain why it is not possible for a magnetic field to do work on a charged particle.
6. A beam of electrons is observed to move in a circular path with radius 3.7 cm in the presence of a uniform magnetic field of 1.6 mT. The electrons have a speed of 1.0 × 107 m/s. This information is used to solve for the properties of the electron. (a) Solve for the ratio of the charge on the electron to its mass. (e/m = ?) (b) Use the accepted value of the charge on an electron to solve for its mass based on this data. (c) Make a sketch showing the circular path of the electrons and the correct orientation of the magnetic field that would result in such a path.
7. The aurora borealis is caused by charged particles colliding with the atoms in the Earth’s atmosphere. Before the collision the charged particles are thought to “spiral in” along Earth’s magnetic field. Suppose such a particle has an energy of 2.0 keV and the magnetic field in that region has magnitude 0.40 G. Solve for the radius of its helical path if the particle is: (a) an electron or (b) a proton.
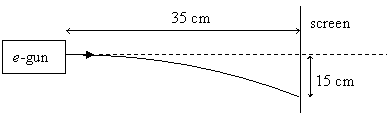
8.
Magnetic
fields are used inside a picture tube to control the stream of electrons
emitted by the electron gun. Suppose the electrons are accelerated by a
potential difference of 18 kV. In order to cause the stream to follow the
curved path shown below, what must be the magnitude and direction of the
magnetic field assuming it to be constant between the gun and the screen?
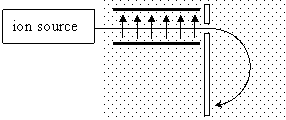
9.
One type of
mass spectrometer uses the layout shown below. The dots represent a
uniform magnetic field of 0.800 T out of the page. The parallel arrows
represent an electric field of 200 kV/m.
Suppose the source emits hydrogen ions and isotopes are detected at radii of
3.26 mm and 6.56 mm. (a) Find the velocity required of ions to pass
through the electric field without being deflected. (b) Find the masses
of the two isotopes.
10. Refer to the diagram in the previous problem. Suppose singly ionized chlorine atoms are emitted by the source and that two isotopes are present: 17Cl35 (m = 5.85 × 10-26 kg) and 17Cl37 (m = 6.18 × 10-26 kg). The fields are B = 0.50 T and E = 40.0 kN/C. (a) What is the distance between the two points where the ions hit the detector? (By how much are the ions separated?) (b) What design changes would make a mass spectrometer like this one more sensitive to differences in mass? Explain.
11. A uniform magnetic field of 0.300 mT points in the positive x-direction. A wire of length 20.0 cm lies in the xy-plane and passes through the field carrying a current of 75.0 mA. Determine the force on this section of wire if the current is directed toward: (a) 0.0°, (b) 30.0°, (c) 90.0°, (d) 120.0°, (e) 180.0°.
12. A vertical wire 3.00 m long stretches from floor to ceiling and carries a current of 5.00 A upward. Earth’s magnetic field in the room has magnitude 52.5 μT and lies in a north-south plane but points downward at an angle of 65.0° relative to horizontal. (a) Determine the net force on this section of wire. (b) Repeat for a horizontal wire 5.00 m long with a current of 3.00 A flowing from north to south.
13. A rectangular loop of wire consisting of 100 turns is hung from a scale’s hook. The scale indicates it weighs 1.20 N. The bottom end of the loop, which if 3.00 cm wide, is placed between the poles of a horseshoe magnet where the magnetic field is 0.95 T. (a) Estimate the amount of current that must flow in the loop in order for the scale’s reading to drop to zero. (b) Make a sketch showing how the horseshoe magnet should be positioned relative to the loop and its current in order to achieve this. Label the poles of the magnet. (c) What will the scale read if the magnet is then rotated 45° about a vertical axis.
14.
The diagram
below illustrates a bar magnet and four currents in its vicinity. Current
I1 parallels the magnet. Current I2
runs across one end. Current I3 passes behind and
midway between the poles. The axis of the square loop current I4
is aligned with the axis of the magnet. Describe in specific but
qualitative terms the net force and/or net torque on each current.

15.
A
rectangular loop of wire, dimensions 10.0 cm × 5.00 cm, lies in a nonuniform magnetic field, as shown in the diagram
below. The magnitude of the magnetic field is given by B = 0.25/y,
where B is in mT and y is in
centimeters (it does not vary in the x-direction). The field
points into the page. Determine the net force on the loop of wire
if: (a) it carries a current of 2.00 A
clockwise, (b) it carries a current of 4.00 A counterclockwise.

16. A square coil of wire has sides of length 3.00 cm and 80.0 turns and lies in the xy-plane. The coil lies in a magnetic field of 0.100 T directed in the positive y-direction. (a) Determine the torque on the coil if it carries a current of 2.00 A in a clockwise direction. (b) Suppose the coil rotates 30.0° in the direction of the torque – find the new value of the torque’s magnitude.
17. Suppose the coil in the previous problem is a rectangular coil that has an area equal to that of the square. Make the width and length any appropriate combination of values (so that area is 9 cm2). (a) Calculate the amount of force on each side of the rectangular coil. (b) Use the force values to calculate the torque about a horizontal axis and show that the result is the same as part (a) of the previous problem.
18.
A
demonstration motor is formed by winding 300.0 turns in a circular loop of
diameter 1.50 cm. The loop can turn around an axle of diameter 2.00 mm as
shown in the diagram below. The loop is placed in a uniform magnetic
field of 0.25 mT. The entire rotor assembly has
mass 50.0 g and the coefficient of friction between axle and support is
0.050. (a) Estimate the maximum possible angular acceleration if the
current is set at 3.00 A (use moment of inertia I = ½ MR2).
(b) What is the minimum current that can set the rotor into motion?
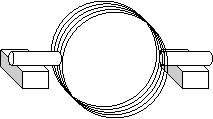
19. A current of 3.00 A flows through a segment of wire from the origin to a point with coordinates: (0.500 m, 0). Determine the magnetic field produced by this segment at positions in the xy-plane: (a) (0.250 m, 0.100 m), (b) (0.250 m, 0.200 m), (c) (0.500 m, -0.200 m), (d) (0.750 m, 0).
20. Repeat the previous problem for an infinitely long current of the same amount running in a positive direction all along the x-axis and compare to the results for the finite current. At which position are the two values closest to one another? Why?
21. A square shaped coil of wire has 30.0 turns and sides of length 10.0 cm. (a) Determine the magnetic field at the precise center of the square if a current of 4.00 A is sent clockwise through the coil. (b) Would the center be the location of the maximum field strength? If not, where do you think the field would be greatest and why? Support your response either way.
22. Suppose you want to create a magnetic field of 5.00 mT at the center of a circular coil of wire with radius 3.00 cm that carries a current of 2.00 A. (a) How many turns are required? (b) If the wire is copper with diameter 0.300 mm, what voltage battery would be needed to achieve this level of current?
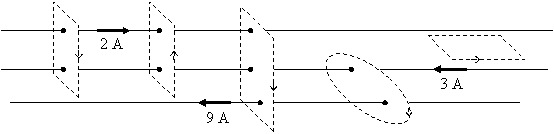
23.
Examine the
figure shown below, which shows a continuous loop of current. Find the
magnetic field at point P as a function of current I and radii a and b.

24.
Determine
the magnetic field at the tip of the cone shown below. A current I
loops the base in a circle of radius R. Express the result in
terms of I, R, θ, and fundamental
constants.

25. A long straight wire of diameter 1.60 mm carries a current of 10.0 A. Find the magnetic field strength at distances from the center: (a) r = 0.400 mm, (b) r = 0.800 mm, and (c) r = 1.20 mm.
26.
Examine the
currents in the diagram and determine the result of the integral ![]() for
each path shown.
for
each path shown.
(a)
(b)
(c)
(d)
(e)
27. Two long parallel wires carry the same amount of current, I, and are separated by distance a. One wire runs along the z-axis and the other is at x = a. Both currents are in the positive z-direction. (a) Sketch the resulting magnetic field in the xy-plane. (b) Derive an expression for the magnetic field at any point x along the x-axis. (c) Find the magnetic field at coordinates (a/2, a/2, 0).
28. Repeat the previous problem but this time the wire at x = a has current I in the negative z-direction.
29.
A long wire
carrying a current of 4.00 A is arranged vertically in a room, stretching from
floor to ceiling. When held anywhere on the east side of the wire, the
compass points precisely north, as shown in the diagram (an overhead
view). Given the Earth’s magnetic field in this room is 0.500 G, north,
determine the direction the compass will point when held: (a) 5.00 cm
north of the wire and (b) 10.0 cm north of the wire. (c) At what
position(s) relative to the wire would a compass point due south?

30.
A certain
coaxial cable has a conducting wire running down the center and a conducting
cylindrical “sheath” surrounding the wire, as shown in cross section below (not
to scale). Suppose a current 2I flows through the center wire and
a current I flows in the opposite direction
through the sheath. (a) Determine the magnetic field as a function of r,
the radial distance from the center. (b) Sketch the graph of magnetic
field vs. radial distance.

31. Refer to the diagram from the previous problem. Suppose at each end of the cable the wire is electrically connected to the sheath and the two conducting parts of the cable carry a total current of 10.0 A in one direction. Use dimensions of a = 1.00 mm, b = 4.00 mm, and c = 5.00 mm. Find the magnetic field strength at each distance from the center: (a) r = 0.500 mm, (b) r = 4.00 mm, and (c) r = 4.50 mm. Hint: you must determine what fraction of the total current flows in each part of the cable.
32. A long straight wire carries a current of 15 A along the x-axis in a positive direction. An electron at position r = 0.10 j m has velocity 2.0 × 107 i m/s. (a) Find the magnetic field at the electron’s position. (b) Find the acceleration of the electron. (c) Find the instantaneous radius of curvature of the resulting path of the electron’s motion. (d) Sketch the path the electron would follow.
33. A long straight wire is taped to the floor and carries a current of 20.0 A. A second wire is located 1.00 cm directly above and parallel to the first wire. (a) Find the force per length on the second wire if it carries 10.0 A in the same direction as the other current. (b) If the second wire has mass per length 0.12 g/cm, what current would be required in it to cause it to “levitate” above the first wire (without any other means of suspension)?
34. The power cord for a certain household device consists of two parallel wires separated by 3.5 mm. When in use, the cord carries 5.0 A “down and back” – the same amount flowing in opposite directions. (a) Find the force per length and describe as attraction or repulsion. (b) If the power cord is 2.0 m long, estimate the total amount of force on each strand. (c) Household power is alternating current, which means that the direction of the current reverses periodically. Describe and explain qualitatively the effect this would have on the forces in this question.
35.
A current
of 10.0 A flows in a long straight wire. A
rectangular coil of wire with 100 turns and width and length 5.00 cm × 10.0 cm
is brought near the wire as shown in the diagram. The coil carries 5.00
A. (a) Determine the magnitude of the net force on the coil if x =
2.00 cm. (b) At what value of x would the force on the wire
equal half the force on the coil found in part (a). (c) In what direction
should the current in the coil flow if the wire is to be repelled by the coil?

36. A certain cylindrical solenoid has length 10.0 cm, radius 2.00 cm, and 275 turns of wire. (a) Estimate the magnetic field inside this solenoid if it carries a current of 3.00 A. (b) What current in this solenoid would be needed to produce a field of 0.100 T?
37. A student plans to make a solenoid using copper wire of diameter 0.644 mm (22 gauge) that has an insulating coating of negligible thickness. The wire will be wrapped around a cardboard tube of diameter 4.20 cm and length 28.0 cm (from a roll of paper towels). The solenoid will be wrapped as tightly as possible with single loops from one end to the other. The solenoid will be powered by a 6.00 V battery with internal resistance 1.50 Ω. (a) How many turns will fit on the tube? (b) What length of wire is needed for the project? (c) What strength magnetic field can be produced? (d) If a stronger magnetic field than this is desired should the student use wire with a greater or lesser diameter? Explain.
38.
A toroidal solenoid consists of wire loops in the form of a
donut shape (a torus). It also may be imagined as a flexible cylindrical solenoid
that has been bent into a circular ring so that the ends meet. The
solenoid has N turns of wire and inner radius R1 and
outer radius R2 as shown below. Use Ampere’s Law to
solve for the magnetic field as a function of r, the perpendicular
distance from the axis of the torus.

39. A certain toroidal solenoid has characteristics of N = 500 turns, R1 = 5.00 cm, R2 = 8.00 cm, I = 5.00 A. (a) Find the minimum and maximum magnetic field strength that occurs inside the torus. (b) Make a careful sketch of the graph B vs. r.
40. An electromagnet is formed by wrapping a solenoid around an iron core. Suppose an electromagnet with 35 turns per centimeter carries 0.20 A current and produces a field of 0.90 T with the core in place. (a) Find the magnetic field that would be produced without the core in place. (b) By what factor does the core increase the strength of the magnet? (c) What type(s) of motion must the electrons inside the core undergo to explain this increase? Explain. (d) If the iron is replaced with aluminum (which is paramagnetic) what will be different? Explain.
41. Consider the field created by a horseshoe magnet (you can find a diagram online here). Apply the domain model to explain the field of such a magnet: (a) Sketch the arrangements of domains within the horseshoe. (b) The field is very strong in the space directly between the two ends of the horseshoe -- how does this make sense considering domains throughout the metal?
42. How is a horseshoe magnet manufactured? Discuss two possibilities: (a) Iron in the shape of a horseshoe is subjected to a strong external magnetic field with the correct properties – what should these properties be and what might produce such a field? Explain. (b) Iron in the shape of a straight rod is first magnetized and then bent into the shape of a horseshoe – considering the domain model do you think this would work? Explain.
43. An ordinary iron nail can be turned into a permanent magnet by subjecting it to an external magnetic field. For the best results align the originally “neutral” nail parallel to the external field. But why is that “better” than arranging the nail perpendicular to the external field? Wouldn’t the domains in the nail still orient to the external field? Discuss and explain.
44. The effect of diamagnetism helps explain a classic physics demo – an ordinary permanent magnet will float in midair if it is placed directly over a superconducting disk. The superconductor is very diamagnetic. (a) Sketch the field and poles of the permanent magnet and the resulting magnetic properties of the superconductor. (b) Refer to your sketch to explain the force that opposes gravity on the magnet. (c) What would determine the distance between the floating magnet and the superconductor?
1. a. b. c.
2. a. b.
3.
a. 1.25 ×
10-10 N, north
b. 2.50 × 10-10 N, down
c. 1.25 × 10-10 N, down
d. 0
4.
![]()
5. a. b.
6.
a. 1.69 ×
1011 C/kg
b. 9.5 × 10-31 kg
(4.1% error)
c.
7.
a. 3.8 m
b. 160 m
8. 9.4 G, into the page
9.
a. 250
km/s, right
b. 1.67 × 10-27 kg (1H1)
3.36 × 10-27 kg (1H2)
10. a. 6.6 mm
b.
11. a. 0
b. -2.25 k μN
c. -4.50 k μN
d. -3.90 k μN
e. 0
12. a. 0.333 mN, west
b. 0.714 mN, east
13. a. 0.42 A
b.
c. 0.35 N
14. I1 net force = 0,
net torque in -j dir.
I2 net torque = 0,
net force in +i dir. (depending on length)
I3 net torque = 0,
net force in -i dir.
I4 net torque = 0,
net force in -k dir.
15. a. -10 j μN
b. 21 j μN
16. a. 0.0144 i Nm
b. 0.0125 i Nm
17.
18. a. 11 rad/s2
b. 1.8 A
19. a. 5.57 k μT
b. 2.34 k μT
c. −1.39 k μT
d. 0
20. 6.00 k μT, 3.00 k μT,
−3.00 k μT
21. a. 1.36 mT into page
b.
22. a. 119
b. 10.6 V
23. ![]() , into page
, into page
24. ![]() , up
, up
25. a. 1.25 mT
b. 2.50 mT
c. 1.67 mT
26. a. −1.3 × 10−6
Tm
b. 1.3 × 10−6 Tm
c. −1.3 × 10−5 Tm
d. −1.5 × 10−5 Tm
e. 0
27. a.
b. ![]()
c. ![]()
28. a.
b. ![]()
c. ![]()
29. a. 17.7° Wof N
b. 9.1° W of N
c. r <1.6 cm W of wire
30. a. 
b.
31. a. 1.00 G
b. 0.500 G
c. 2.33 G
32. a. 3.0 × 10−5
k T
b. 1.1 × 1014 j m/s2
c. 3.8 m
d.
33. a. 4.00 × 10−3
N/m, down
b. 294 A, opp. dir.
34. a. 1.4 mN/m, repulsion
b. 2.9 mN
c.
35. a. 2.08 mN
b. 3.54 cm
c. CCW
36. a. 10.4 mT
b. 28.9 A
37. a. 434
b. 58.2 m
c. 2.61 mT
d.
38. 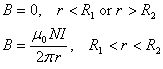
39. a. 6.25 mT, 10.0 mT
b.
40. a. 0.88 mT
b. 1000 times
c.
d.
41. a. b.
42. a. b.
43.
44. a. b. c.