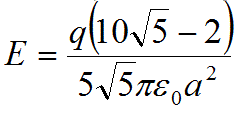AP Physics C Assignment – Electrostatics
Reading Physics for Scientists and Engineers Chapters 22 and 23
Objectives/HW
|
|
The student will be able to: |
HW: |
|
1 |
Relate electrical phenomena to the motion and position of the fundamental charge found on electrons and protons and explain process of charging in terms of conduction or induction and relate to properties of conductors and insulators. |
1 – 6 |
|
2 |
State and apply Coulomb’s Law to solve problems relating force and separation of discrete charges and recognize the coulomb as the SI unit of charge and e as the elementary quantum of charge. |
7 – 15 |
|
3 |
Define and apply the concept of electric field in terms of force acting on a charge within the field and solve related problems |
16 – 19 |
|
4 |
Solve problems involving the motion of a charged particle in a uniform electric field. |
20 – 24 |
|
5 |
Determine the electric field produced by a discrete charge or a set of such charges and solve related problems. |
25 – 29 |
|
6 |
State and apply the rules for sketching electric fields. |
30 |
|
7 |
Determine the electric field produced by a continuous charge distribution and solve related problems. |
31 – 42 |
Homework Problems
1. It is found that an amber rod becomes negatively charge by rubbing it with the fur of a rabbit. (a) Explain what has happened to electrons in this process. Is this conduction or induction? (b) What must be true of the net electrical charge of the rabbit fur?
2. It is found that a glass rod becomes positively charge by rubbing it with a piece of silk cloth. (a) Explain what has happened to electrons in this process. Is this conduction or induction? (b) What must be true of the net electrical charge of the silk?
3. Suppose you have an amber rod, a glass rod, and a piece of fur – all initially uncharged (electrically neutral). You rub the amber with the fur and then rub the glass rod with the fur. (a) Predict what charge (+, −, or neutral) will exist on all three objects after this sequence of events. (b) Explain your reasoning.
4. A glass rod is rubbed with a piece of silk. The rod is brought near to a neutral pith ball. It is observed that the ball is at first attracted to the rod. But as soon as the ball touches the rod it is repelled by the rod. (a) Explain why the ball is initially attracted to the rod before it touches. (b) Explain why the ball is repelled by the rod after it touches.
5. A rubber balloon can become charged by rubbing it on hair. Once it is charged it is observed that small pieces of paper, initially uncharged, can become stuck to the balloon. (a) What type of charge would be obtained by the balloon? Explain your reasoning. (b) Explain why the electrically neutral pieces of paper would be attracted to the balloon.
6. A lightning rod is a metallic conductor that connects to the earth and extends above the roof of a building. When a negatively charged cloud is nearby, a positive charge is induced in the extended end of the rod. (a) Explain how and why this happens. (b) Explain why lightning will likely strike the rod (instead of something else). (c) Would the lightning rod work if the cloud were positively charged? Explain.
7. Suppose a hollow aluminum sphere of mass 100.0 g and radius 10.0 cm is given a net charge of −1.00 μC by a Van de Graaff generator. (a) Determine the difference between the number of electrons and protons in the charged sphere. Of which is there more? (b) Given that aluminum is element 13 and has atomic mass 26.98 g/mol, determine the percentage of atoms in the sphere that are singly “ionized”. (c) Assuming the net charge is spread evenly across the surface of the sphere, calculate σ, the charge density per area. (d) Explain why the net charge would be spread evenly across the surface of the sphere since it is a conductor. (e) How many coulombs of positive charge exist in the sphere?
8. Two charged pith balls, q1 = −3.0 nC and q2 = −2.0 nC, are separated by 15.0 cm. Find the force on each ball and describe it as attraction or repulsion.
9. A certain pith ball of mass 0.11 g has a charge of +2.5 nC and is suspended by a string over the top of an aluminum sphere with charge +4.0 μC. As the ball is lowered the tension in the string decreases. At what minimum height from the center of the sphere would the tension in the string be zero (at which point the ball is levitated by electric force)?
10. A pith ball of mass 0.25 g and charge −1.5 nC is dropped by the side of a sphere with charge +3.0 μC. Determine the acceleration of the pith ball when it reaches a position 0.300 m to the right of the sphere’s center.
11. Three point
charges are arranged in a line as shown below: q1 = +4.0 nC,
q2 = −2.0 nC, q3 = −1.0 nC.
Determine the net electric force on each.

12. A charge q is placed on the x-axis at x = −a. Where could a second charge, nq, be placed such that any third charge placed at the origin would experience a net electric force of zero? (a and n represent positive quantities, q can be positive or negative)
13. Two identical pith
balls hanging from strings are each touched by a charged glass rod and then
attain the equilibrium state shown in the diagram below once the glass rod is
removed from the area. (a) Solve for the charge on each pith ball, assuming
each has the same amount. (b) Supposing one has twice the charge of the other,
what is the charge on each?
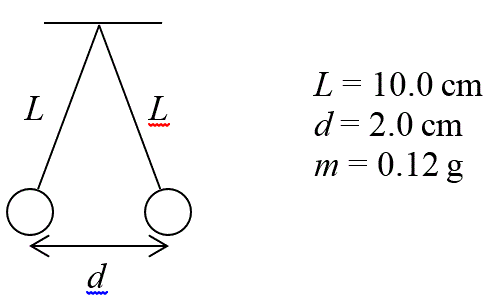
14. Consider the glass rod in the previous problem. How many electrons total were lost or gained by the rod in the interactions with the pith balls? Calculate this value for part (a) and part (b) and state as a loss or gain. (c) What observation(s), if any, of either the rod or the pith balls could be made in order to determine whether or not the pith balls received equal amount of charge? Explain.
15. Four charges are
arranged at the corners of a square of side a. Each charge has
magnitude q but two are positive and two are negative as shown in the
diagram below. Find the force on each of the charges in terms of εo,
q, and a.

16. A pith ball with charge −1.5 nC experiences an electrostatic force of 0.45 mN, leftward when placed at a certain position. (a) Determine the electric field at that position. (b) If a different pith ball with charge +2.0 nC is placed at the same position, what force will act on it?
17. In certain experiments, a Van de Graaff generator can produce an electric field with a strength of 3.0 × 106 N/C. Explore the effect of such a field on a hydrogen atom composed of one proton orbited by one electron: (a) Calculate the amount of force that would act on the proton. (b) How would the force on the electron compare to this? (c) Find the force of attraction between the proton and electron given the radius of the hydrogen atom is 5.3 × 10−11 m. (d) Would this electric field be strong enough to ionize the atom (i.e. separate the electron from the proton)? This is not as simple as it might seem.
18. The dielectric strength of air is 3.0 × 106 N/C. This is the strength of electric field that will cause ionization to occur in the molecules that comprise the air. And it is the minimum electric field required for an electric spark to move through air. So, whenever a spark is observed to be issued from a Van de Graaff generator one can surmise that the electric field is at least 3.0 × 106 N/C – explain what is happening to the air in the region of the spark.
19. The Earth is surrounded at its surface with a very weak electric field of 150 N/C downward. (a) Find the net force (electrostatic and gravitational) on a proton (m = 1.67 × 10−27 kg) near the surface of the Earth. (b) What percent error would be introduced by ignoring the force of gravity? (c) What would happen to this percentage if the electric field were stronger?
20. In Millikan’s oil drop experiment tiny drops of oil were observed drifting through air in a small chamber between two horizontal parallel metal plates. The drops of oil experienced drag given by Fd = −kv, where k = 1.60 × 10−10 kg/s. At first the oil drops were observed falling at terminal velocity. Then x-rays ionized the oil drops and a voltage was applied to the plates creating an electric field. In the presence of the electric field the charged oil drops were observed rising at a different terminal velocity. Suppose a particular drop was observed falling at 0.200 mm/s and then rising at 0.297 mm/s in the presence of an electric field of 125 kN/C, down. (a) Find the mass of the oil drop. (b) Find the charge on the drop. (c) How many excess electrons are on the drop?
21. Suppose the same oil drop from the previous problem were to lose a single electron (instead of gaining four) in the ionization process – what would be its terminal velocity in the presence of the electric field?
22. In a certain TV picture tube, an electron (m = 9.11 × 10−31 kg) is accelerated across a distance of 20.0 mm by an electric field of 750 kN/C. Assume the electron is initially at rest. (a) Find the acceleration rate of the electron. (b) Find the speed attained by the electron. (c) Repeat for a proton in the same circumstances.
23. Two parallel metal
plates are given opposite charges such that a uniform electric field of strength
E exists between the plates. A particle of mass m, charge e,
and speed v, enters the field moving parallel to the plates as shown in
the diagram below. (a) Find the vertical displacement y that the particle
is deflected from its original path. (b) Find the angle θ by which
the particle is deflected from its original direction of travel.

24. Suppose a beam of charged particles, each with energy 15 keV and charge e, enters the space between two oppositely charged parallel circular plates of diameter 10.0 cm separated by 2.0 mm. (a) Determine the maximum deflection angle possible – direction of exit beam versus that of entrance beam. (b) What is the required field strength?
25. Determine the electric field strength at points 10.0 cm, 20.0 cm, and 30.0 cm away from a point charge of + 4.0 nC.
26. An electric dipole consists of two equal and opposite charges separated by a relatively small distance. Suppose there is a dipole consisting of point charges −3.00 nC located at coordinates (−5.00 cm, 0) and +3.00 nC located at (+5.00 cm, 0) in the xy-plane. Find the net electric field produced by this dipole at the following locations in the xy-plane: (a) (0, 0), (b) (0, 5.00 cm), (c) (−15.0 cm, 0), (d) (75.0 cm, 0), (e) (5.00 cm, 5.00 cm).
27. The electric dipole moment p = qs can be used to approximate the field of a dipole at a distance r along a perpendicular bisector. (a) Show analytically that this approximation is given by E = kp/r3 for r >> s. (b) Determine the field of the dipole from the previous problem at coordinates (0, 75.0 cm). (c) Determine the force on a water molecule at a position 50.0 cm, 0.0° from a pith ball of charge 3.0 nC, given pH2O = 6.2 × 10−30 Cm, 90.0°.
28. A positive point charge of 8.0 nC is placed at x = −20.0 cm on a number line. A negative point charge of −2.0 nC is placed at the origin. (a) Find the net electric field at x = 10.0 cm. (b) At what point along the number line would the field be zero? (c) Determine the maximum field on the line for points x > 20.0 cm. (d) At great distances from these two charges (in any direction) the field would be essentially equivalent to that produced by a single charge of what value placed at the origin? Explain or support your answer mathematically.
29. Find the magnitude of the net electric field at a midpoint of one side of the square from problem #15.
30. (a) Sketch the electric field surrounding the charges in problem #15. (b) Sketch the electric field surrounding the two charges in problem #28.
31. A thin rod of length 20.0 cm is given a uniform charge of −50.0 nC. (a) Determine λ, the charge per unit length, in C/m. (b) Find the electric field at a position 30.0 cm from the center along the axis of the rod. (c) Determine the force on a pith ball of charge +2.00 nC placed at that position.
32. For a thin rod of length 20.0 cm and uniform charge −50.0 nC: (a) Find the electric field at a position 30.0 cm from the center along a perpendicular bisector. (b) Find the electric field 1.00 cm from the center along a perpendicular bisector.
33. Approximate each field value of the previous problem by: (a) Assuming the rod is a point charge at a distance of 30.0 cm. (b) Assuming the rod is of infinite length at a distance of 1.00 cm and use E = λ/(2πεor). (c) Find the percent error in each approximation.
34. A wire of length 0.500 m is given a uniform charge of +1.00 μC. The wire lies along the positive x-axis with one end on the origin. (a) Find the x-component of the electric field at position: (0, 0.200 m). (b) Find the y-component of the electric field at the same point.
35. Sketch the electric field surrounding a thin negatively charged rod.
36. A charge Q
is distributed uniformly along a thin semicircular ring of radius R.
Find the electric field at the center of this arc of charge.

37. Sketch the electric field surrounding the semicircular charge from the previous problem.
38. A charge of 2.0 μC is spread uniformly on a circular surface of diameter 0.840 m. (a) Find the charge density (per area) on the surface. (b) Estimate the electric field strength a few millimeters above the center of the surface.
39. A charge of 2.0 μC is spread uniformly on both sides of a thin metal circular plate of diameter 0.840 m. (a) Find the charge density (per area) on the surfaces. (b) Estimate the electric field strength a few millimeters above the center of one side of the plate.
40. Two square aluminum plates are mounted parallel to one another and separated by 2.00 mm. The plates are each 10.0 cm on a side. One plate is given a charge of +7.00 nC and the other is given a charge of −7.00 nC. (a) Essentially all of the net charge on either plate will move to one surface – which surface and why? (b) Find the charge per area on either charged surface. (c) Estimate the electric field strength between the two plates. (d) Explain why the field is essentially zero for regions outside of the plates.
41. Two parallel circular metal plates of radius 3.00 cm are separated by 1.00 mm to form an electron gun. In order to “fire” an electron at 2.0 × 107 m/s, what must be the amount of charge on each plate?
42. Suppose positive charge is distributed uniformly with density λ all along the y-axis and with the same density along only the negative portion of the x-axis. Find the electric field as a function of x along the positive x-axis.