AP Physics Assignment – Dynamics: Forces and Newton’s Laws of Motion
Reading Physics for Scientists and Engineers – Chapters 5, 6, 7: pp. 110 – 184
Objectives/HW
|
|
The student will be able to: |
HW: |
|
1 |
State
|
1 – 7 |
|
2 |
Recognize and state the proper SI unit of force and give its equivalence in fundamental units and use the relation Fnet = ma to solve problems. |
8 – 10 |
|
3 |
Recognize the difference between weight and mass and convert from one to the other. |
11 – 14 |
|
4 |
State
and utilize |
15 – 18 |
|
5 |
Understand and utilize the concept of the normal force to solve related problems. |
19, 20 |
|
6 |
Define and apply the concepts of compression and tension and use the method of sections to solve for these. |
21 – 26 |
|
7 |
Solve force problems involving pulleys, including those involving multiple objects and systems of equations (such as Atwood’s machine). |
27 – 31 |
|
8 |
Understand and utilize the relation between friction force, normal force, and coefficient of friction for both cases: static and kinetic. |
32 – 37 |
|
9 |
Solve problems involving air resistance in which friction is assumed directly proportional to velocity; define and apply the concept of terminal velocity. |
38 – 40 |
|
10 |
Apply the concept of force components to objects on an incline and solve related problems. |
41 – 46 |
Homework Problems
1.
A classic “parlor”
trick is to grab a tablecloth and pull it out from under the plates,
silverware, and tumblers of a full dinner setting. If done properly, all
of the place settings hardly move as the tablecloth is pulled out.
Explain how this trick “works” in light of
2. Describe the type of path that must be followed by an object moving in the absence of force. Explain.
3. Must an object always move in the direction of the net force acting upon it? Explain and give examples to support your answer.
4.
A cart on
wheels is loaded with books. In order to move the cart you must exert a
relatively great force to start it moving but then a much smaller force to keep
it moving. Use
5. In order for an object to move at greater and greater speeds does it require a greater and greater amount of force? Explain your answer using the laws of motion.
6.
Consider
what happens when a car collides with a tree and the passenger in the front
seat is not wearing a seatbelt. Refer to
7. In an old pickup truck there may be a window directly behind the driver’s head – often with no headrest. If such a truck is at rest and is hit from behind by another car, the driver’s head is likely to impact the window behind it. (a) Explain why this happens. (b) Would the result be different if the truck was initially in motion instead of at rest? Explain.
8. A Mini Cooper has a mass of 1290 kg and can go from 0 to 26.8 m/s in 6.2 s. What average amount of net force must act on the car in order for this to occur?
9. In reality the net force on a car varies as it accelerates. The net force on the Mini from the previous problem can be modeled by F = 6579 − 387t, where F is in newtons and t is in seconds, when it is accelerating maximally from rest. (a) Find the maximum amount of acceleration. (b) Find the magnitude of acceleration and speed at t = 2.00 s. (c) Determine the time for it to go from zero to 20.0 m/s. (d) Determine the time for it to go from 20.0 m/s to 40.0 m/s.
10. In a physics experiment an object is observed to accelerate 2.5 m/s2, 0.0° when under the influence of two forces: F1 = 5.0 N, 0.0° and F2 = 1.5 N, 180.0°. Determine the mass of the object.
11. A toolbox of mass 3.2 kg is lowered by rope from the roof to the ground. Find the acceleration of the toolbox when the force of the rope is: (a) 40.0 N and (b) 20.0 N.
12. A package that weighs amount W is lifted by a person and accelerates upward amount a. What force F must the person exert for this to happen? Derive an expression.
13. David Blaine performed a
stunt in which he fell from atop a 27 m pole onto a stack of cardboard
14. A girl throws a 175 gram softball by exerting upon it a force of 10.0 N, 45.0°. (a) Determine the resulting acceleration of the softball. (b) Repeat for the same amount of force applied by the girl in a downward direction.
15. Identify and describe at least one action-reaction pair of forces in each of the following scenarios: (a) A person climbs a ladder. (b) A propeller-driven airplane flies. (c) A soccer ball is kicked. (d) A car accelerates from a stoplight.
16. In order for a 70.0 kg
sprinter to accelerate 4.00 m/s2 eastward, what force must he exert
on the blocks at the starting line? Explain how
17. An apple of mass 444 g breaks loose of a tree and falls for 1.11 s before being caught by a person. The person’s hand is moved downward 9.99 cm by the apple as it is caught. (a) Describe the action-reaction pairs of forces for the apple and the earth and for the apple and the hand. (b) Find the amount that the earth (m = 5.974 × 1024 kg) moves upwards while the apple is falling. (c) Find the average amount of force that the apple exerts on the person’s hand.
18. According to the 2nd Law it is necessary to have a net force in order for any object to accelerate. According to the 3rd Law forces always occur in pairs that are equal and opposite. If these concepts apply to all things, it might seem that no object could ever accelerate because every force that may act on it is countered by an equal and opposite force, which would yield a net zero force. Explain why this is a false notion.
19. A basketball that weighs 5.84 N is dribbled on the floor. In the process of bouncing the ball has an acceleration of 80.0 m/s2 upward. (a) Determine the normal force the floor exerts on the ball. (b) Determine the normal force that the ball exerts on the floor.
20.
A metal box
is tilted at an angle of 30.0° as shown below. Inside the box rests a
bowling ball of mass 5.00 kg. Determine the normal force at each point of
contact.
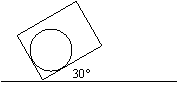
21.
A traffic signal
of mass 25.0 kg is suspended by two cables as shown in the diagram below.
Solve for the tension in each cable each of the following scenarios: (a)
θ1 = θ2 = 20.0°, and (b)
θ1 = 20.0°, θ2 = 30.0°.

22.
A pair of
fuzzy dice hangs from the ceiling of a car with acceleration a as shown.
Assuming the dice have the same acceleration as the car, derive an expression relating
θ to a and g.

23. Suppose there is a stack of ten books on the floor. Each book has a mass of 1.40 kg. (a) Determine the force that the eighth book exerts on the ninth book. (count up from the bottom) (b) Determine the force that the second book exerts on the first. (c) Find the normal force the first book exerts on the floor if a boy with mass 60.0 kg jumps off the top of the stack with an acceleration of 3.00 m/s2, upward.
24. A man of mass 95.00 kg is hanging from the end of a rope of mass 2.50 kg. The other end of the rope is attached to a helicopter. If the helicopter rises such that the man accelerates upward at 4.000 m/s2 find the tension in the rope at its: (a) bottom, (b) middle, and (c) top.
25. Consider a man standing in an elevator. The man has a total mass of 70.0 kg. Each of his legs has a mass of 12.0 kg. (a) If the elevator is at rest determine the normal force on each foot and the amount of vertical force at the joint of each femur and pelvis. (b) Repeat with the elevator accelerating upward at 2.00 m/s2. (c) Repeat with the elevator accelerating downward at 1.5 m/s2.
26.
Two balls
of mass m1 and m2 are connected by a string
and lifted by an upward force F as shown below. Derive and
simplify an expression for the tension T in the connecting string in
terms of relevant variables and constants. The result should allow for
the possibility of acceleration. Do not ignore gravity.

27.
Two objects
are connected by a cord of negligible mass that passes over a massless, frictionless pulley as shown below. When
the two objects are released, the object with mass 700.0 gram accelerates
downward at 3.00 m/s2. (a) Determine the mass of the other
object. (b) Find the tension in the cord as the objects move.
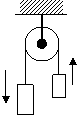
28.
A window
cleaner of mass 75.0 kg lifts himself and his 25.0 kg platform by the rope and
pulley system shown in the diagram below. (a) In order to go up at a
constant velocity what force must he exert on the rope? (b) Determine the
amount of normal force on his feet as he rises at constant velocity. (c) Find the acceleration if the man pulls 525 N on the rope.

29.
Two
objects, masses 6.0 kg and 8.0 kg, are connected by a lightweight cord that
passes over a massless, frictionless pulley as shown
in the diagram. An upward force of 250.0 N acts on the axle of the pulley, causing the entire system to move upward (the pulley
is still free to rotate). Determine the acceleration of each mass and the
acceleration of the pulley.
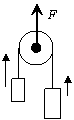
30.
A truck of
mass 2250 kg is used to pull a 330 kg trunk out of an old quarry as shown
below. There is 550 N of rolling resistance for the truck. Ignore
mass and friction of the pulley. (a) If the trunk is accelerated upward
at 2.00 m/s2 what is the minimum amount of horizontal force the
truck’s drive wheels exert on the ground? (b) For the same conditions
what is the tension in the towrope?

31. Suppose the truck in the previous problem pops out of gear and is momentarily in neutral such that it is pulled back by the trunk. (a) Find the resulting acceleration. (b) Find the tension in the rope.
32. Two boys stand on the surface of a frozen lake where μs = 0.15 and μk = 0.10. The 30.0 kg boy shoves the 40.0 kg boy with a horizontal force of 50.0 N, 0.0°. Find the resulting acceleration of each boy.
33. A man of mass 80.0 kg pushes horizontally on a large crate as he moves it across a level floor where μk = 0.30. When the man’s feet push against the floor 300.0 N to the left, the man and the crate both accelerate 1.50 m/s2 to the right. (a) Find the force that the man exerts on the crate. (b) Find the mass of the crate.
34.
A block of
mass m is pulled across a level surface by a rope that makes an angle
θ with the horizontal. The coefficient of friction is μ.
(a) Determine the amount of force F required to slide the block at a
constant velocity. (b) Determine the optimum angle at which to pull on
the block (so that the required force is minimized). (c) If the force of
the rope is 15.0 N acting on a block of mass 2.00 kg where μ = 0.35, what
is the maximum acceleration possible?

35. A man pushes 100.0 N on the handle of a 40.0 kg lawnmower. The applied force is in the same direction as the handle, which is tilted 35.0° relative to horizontal. The coefficient of kinetic friction is 0.10. Find the amount of acceleration.
36. A large crate sits in the back of a pickup truck. The coefficients of friction are: μs = 0.60 and μk = 0.40. (a) Find the maximum forward acceleration of the truck at which the crate will not slide backward. (b) Suppose the truck decelerates at 8.0 m/s2 and the crate slides 1.5 m forward before hitting the front end of the bed. Find the impact speed (relative to the truck).
37. Friction or “retarding” forces on a car comes in three types: rolling resistance, air resistance, and internal friction associated with the engine and transmission. On a particular small car of mass 900 kg, rolling resistance can be modeled with a coefficient μ = 0.024 and the equation: Ff = μFN. (a) If this car can accelerate from 0 to 25 m/s in 9.0 s with a single 100.0 kg driver, find the time for the same change in speed with three additional passengers of the same mass. (b) Justify the assumptions that must be made about air resistance, "internal" friction, and the force driving the car forward in order to work part (a).
38. A rock of mass 0.400 kg is released from the surface and sinks in the ocean. As the rock descends it is acted upon by three forces: gravity, buoyancy, and drag. The buoyancy is an upward force equal to half its weight. Drag from the water can be modeled by F = kv, where k = 0.650 kg/s. (a) Determine the terminal speed of the sinking rock. (b) Determine its depth, speed, and acceleration 1.50 seconds after it is released.
39. A certain plastic ball of mass 0.150 kg has a terminal speed of 20.0 m/s when falling through air. This ball is launched upward at 16.0 m/s. Assume that air resistance is proportional to speed. (a) Determine the initial acceleration of the ball as it is launched. (b) Determine the time it spends rising and the maximum height that it will reach. (c) If the same ball is rolled across a smooth floor with initial speed 16.0 m/s, what distance will it travel before air resistance stops it (ignoring contact friction).
40. Assuming air resistance is proportional to speed, an object released from rest falls with an acceleration rate that can be modeled by a = get/τ, where τ is the "time constant". (a) Derive an expression for the time constant in terms of an object's terminal speed, vt, and any appropriate constants (but not mass). (b) Determine the time, in terms of τ, for a falling object to reach a speed 99% of its terminal value. (c) According to this model, two objects with the same terminal speed but different masses should fall identically with the same time constant. Besides mass, what else must be different about two such objects? Explain.
41. Consider two kids on skateboards coasting down a hill. (a) Ignoring air resistance, derive an expression for the acceleration, a, as a function of: angle of incline, θ, coefficient of friction, μ, and g. (b) According to the result, the mass of the kid should not matter. However, in reality, the more massive kid will usually have a greater acceleration. Assuming air resistance is the reason, explain the difference in acceleration!
42. A small box is at the bottom of a ramp tilted at an angle of 40.0° above horizontal. The box is given a push and it then slides up the ramp 2.0 seconds before sliding back down. The coefficient of sliding friction is 0.15. Find the time for it to slide back to the point at which it was released.
43. A block is set on an adjustable ramp and the angle of incline is increased slowly until the block is observed to start sliding. (a) Solve for the coefficient of static friction, μs, in terms of the maximum angle of incline, θ, at which the block can remain at rest on the ramp. (b) Considering the fact that μs is almost always less than or equal to one, at what amount of incline would there be too little friction to prevent virtually anything from sliding?
44.
A block of
mass 2.00 kg rests on a ramp tilted at 25.0°. Coefficients of friction
for the block/ramp: μs = 0.300,
μk = 0.100. A string passing
over a high quality pulley connects the block with a bucket as shown
below. The bucket contains sand but a hole is punched in the bottom and
it starts to run out. When there is a certain amount of sand left in the
bucket the block starts to move. (a) What mass of sand is left in the bucket
when it starts to move? (b) Find the acceleration rate of the
block/bucket system shortly after motion begins.

45. As shown in the diagram
below, two blocks are connected by a lightweight cord that passes over a
frictionless, massless pulley. The bottom block
has a mass of 2.00 kg and the top block has mass 0.500 kg. The
coefficient of kinetic friction at each sliding surface is equal to 0.10.
The two blocks are release from rest. Determine the acceleration of each
block. 46. A boulder of mass 575 kg
is at rest on a slope of incline 20.0° and coefficients of friction:
μs = 0.50 and μ
k = 0.40. (a) Determine the range of force that could act on
the boulder (applied parallel to the slope) that would not move the boulder. (b)
In order to accelerate the boulder up the slope at 2.0 m/s2 would require how much force?

Selected Answers
1.
2.
3.
4.
5.
6. a. thru d.
7. a. b.
8. 5600 N
9.
a. 5.10 m/s2
b. 4.50 m/s2, 9.60 m/s
c. 4.52 s
d. 7.75 s
10. 1.4 kg
11. a. 2.7 m/s2,
up
b. 3.6 m/s2, down
12. F = W(1 + a/g)
13. 6.1 kN, upward
14. a. 50.7 m/s2,
37.1°
b. 66.9 m/s2, 270.0°
15. a. thru d.
16. 280 N, westward
17. a.
b. 4.49 × 10−25 m
c. 267 N, downward
18.
19. a. 53.5 N, up
b. 53.5 N, down
20. 24.5 N, 30.0° and 42.4 N, 120.0°
21. a. 358 N in each
b. 277 N and 301 N
22. tan θ = a/g
23. a. 27.4 N, up
b. 123 N, down
c. 905 N, down
24. a. 1311 N
b. 1328 N
c. 1346 N
25. a. 343 N ea. foot, 225 N
ea. joint
b. 413 N ea. foot, 271 N ea. joint
c. 291 N ea. foot, 191 N ea. joint
26.
![]()
27. a. 372 g
b. 4.76 N
28. a. 490 N, down
b. 245 N
c. 0.700 m/s2, up
29. 11 m/s2, up
(6 kg)
5.8 m/s2, up (8 kg)
8.4 m/s2, up (pulley)
30. a. 8.9 kN
b. 3.9 kN
31. a. 1.0 m/s2,
back
b. 2.9 kN
32. 0.69 m/s2,
180° (smaller boy)
the larger boy does not move
33. a. 180 N, right
b. 41 kg
34. a. ![]()
b. ![]()
c. 4.5 m/s2, 0°
35. 0.92 m/s2
36. a. 5.9 m/s2,
forward
b. 3.5 m/s
37. a. 12 s
b.
38. a. 3.02 m/s
b. 2.84 m, 2.75 m/s, 0.428 m/s2, down
39. a. 17.6 m/s2 down
b. 1.20 s, 8.66 m
c. 32.7 m
40. a.
b.
c.
41. a. ![]()
b.
42. 2.4 s
43. a. μs
= tan θ
b. 45°
44. a. 0.301 kg
b. 1.54 m/s2
45. big block: 1.75 m/s2
330.0°
small block: 1.75 m/s2 150.0°
46. a. -720 N < F (up slope) < 4600 N
b. 5200 N