AP Physics Assignment – Current and Circuits
Reading Chapters 27 and 28
Objectives/HW
|
|
The student will be able to: |
HW: |
|
1 |
Define current and the ampere, conventional positive current flow, and solve related problems, including those with both positive and negative charge carriers. |
1 – 3 |
|
2 |
Define resistance and the ohm, state Ohm’s Law, and solve related problems involving ohmic and/or nonohmic devices. |
4 – 7 |
|
3 |
Describe and explain factors influencing resistance, state mathematical relation between resistance, length, area, and resistivity or conductivity, and solve related problems. |
8 – 13 |
|
4 |
Solve problems involving current density, electric field, resistivity, drift velocity and/or use these concepts to explain the nature of resistance. |
14 – 16 |
|
5 |
Solve problems involving electric power. |
17 – 21 |
|
6 |
Determine effective resistance of a network of series and/or parallel resistors. |
22 – 24 |
|
7 |
Solve for voltage, current, resistance, and power in DC circuits using Kirchoff’s Laws and/or effective resistance. |
25 – 38 |
|
8 |
Model a cell or battery as an ideal voltage source or as an EMF with internal resistance and a certain terminal voltage, and solve related problems. |
39 – 43 |
|
9 |
Understand operation and properties of voltmeters and ammeters and illustrate proper connections thereof, and solve related problems. |
44 – 46 |
Homework Problems
1. A large potential difference is applied between two electrodes in a gas tube such that it ionizes the atoms of the gas. This results in free electrons and positively ionized atoms. (a) Suppose 4.0 × 1017 electrons and 4.0 × 1017 ions pass through a cross section at the middle of the tube every 0.50 s – what is the net current in the tube? (b) Sketch the tube and illustrate the electric field and the direction of electrons, ions, and current. (c) If the current is reduced to 0.10 A how many ions will pass through the cross section every minute?
2. A fuse is rated at 5.0 A. Current is sent through this fuse to a rechargeable battery. If it takes 1800 C of charge to rejuvenate the battery, what is the minimum time that this can be accomplished without blowing the fuse?
3. A certain car battery is rated at 550 cold cranking amps. This means that the battery can deliver 550 amperes for up to 30 seconds at 0° C in order to start the car. (a) If it delivers its maximum, how much charge has flowed through the circuit? (b) Suppose instead the car starts in 0.75 s – how much charge has flowed in this more typical case?
4. A certain resistor has a resistance of 100.0 Ω. (a) Calculate the voltages required to establish currents of 0.50 A, 1.0 A, and 1.5 A in this resistor. (b) Repeat for a resistance of 300.0 Ω.
5. In a typical lighting circuit a current of 0.83 A flows through a wire and through the filament of a bulb. The voltage across the wire is 42 mV and the voltage across the filament is 120 V. (a) What is the resistance of the wire? (b) What is the resistance of the filament? (c) The wire represents what percentage of the total resistance in the circuit?
6. A certain resistor is rated at 330 Ω. (a) What current will flow through the resistor if it is connected to a 9.0 V battery? (b) If a current of 50.0 mA flows through the same resistor what is the voltage across it?
7. A certain bulb in a flashlight carries a current of 0.18 A when connected to 5.00 V and it carries a current of 0.28 A when connected to 9.00 V. (a) Find the resistance in each condition. (b) Is the bulb an ohmic device? Explain. (c) What causes the change in the resistance?
8. A light bulb will often “blow” or “burn out” just at the instant it is switched on. (a) If the filament is somewhat like a fuse, what must be true of the current in order for it to blow? (b) When is the current in the bulb greatest – when the filament is at a lower temperature or at a higher temperature? Explain. (c) How do these facts explain the blowing of the light bulb?
9. A resistor is formed from a carbon cylinder of length 1.00 cm and radius 1.00 mm. (a) Determine its resistance. (b) If it is desired to make a 10.0 Ω resistor of the same length and material what must be the radius?
10. A resistor is formed by a cylinder of a certain material with a certain length and diameter. (a) In order to double the resistance of the cylinder what must be done to the length? Explain. (b) If instead the diameter is doubled what becomes of the resistance? Explain.
11. Electricians often refer to the resistance per length of certain types of wire. (a) Determine the number of ohms per kilometer of 14 gauge copper wire (diameter = 1.628 mm). (b) If 30.0 m of such wire carries a current of 10.0 A what is the potential difference of one end relative to the other?
12. Suppose the cost of copper rises such that it is desirable to make wire out of aluminum. In order for aluminum wire to have the same resistance per length as copper wire, what must be true of its diameter? Calculate the ratio.
13. A wire sample of length 1.20 m and diameter 0.500 mm is connected to a variable power supply. It is found that the potential difference across the wire is 1.38 V when the current is 225 mA. (a) Find the conductivity of the material. (b) Find the resistivity of the material. (c) The wire is likely made of what material, referring to the table in your book?
14. A silver wire of radius 1.29 mm and length 1.50 m carries a current of 2.0 A. The number of free electrons is given by n = 5.91 × 1028 electrons/m3. (a) Find the current density in the wire. (b) What is the drift speed of the electrons? (c) How much time does it take an electron to traverse the wire? (d) Determine the potential difference from one end of the wire to the other.
15. Suppose the current density in a certain copper wire is 5.0 × 106 A/m2 (a typical value). (a) Find the electric field in the wire. (b) What is the current and voltage if the wire is 3.00 m long and has a diameter of 1.10 mm? (c) Find the drift speed of the electrons in the wire, given n = 8.489 × 1028 electrons/m3.
16. A potential difference of 0.025 V is applied to the ends of a copper sample that is 4.00 m long and which has a square cross section 2.00 mm on a side. (a) Find the resistance of the copper sample. (b) Find the electric field in the sample. (c) Determine the current density.
17. The starter motor in a certain car draws 250 A as the engine is started. The starter is powered by a 12 V battery and it takes 1.5 s of operation to start the engine. (a) Determine the power of the starter. (b) How much energy is used to start the engine? (c) How much charge flows through the starter in the process?
18. A household light bulb is rated at 100 W and has a filament with resistance 144 Ω (when in operation). (a) What is the current in the bulb? (b) In how much time do a billion electrons exit the filament of the bulb?
19. Utility companies measure electrical energy usage in units of kilowatt-hours. A kilowatt-hour is the amount of energy used by a 1 kW device that is in operation for 1 hour. (a) Determine the number of joules equivalent to a kilowatt-hour. (b) Determine number of coulombs associated with a kilowatt-hour, given a voltage of 120 V. (c) Find the current used by a 1 kW device.
20. A typical household has a circuit breaker box (or fuse box) that limits the total current in the house to 150 A. Use a voltage of 120 V. (a) What is the maximum power consumption rate of the entire house? (b) If the household uses an average amount of energy of 25000 kW-hr per year, what is the average total current in use by the house at any one time?
21. A 6.0 V rechargeable battery is rated at 1200 mA-h (the unit combination milliamp-hour is similar to the kilowatt-hour). Suppose this battery is fully charged and is then used to power a flashlight with a 2.0 W bulb. (a) What current flows through the bulb? (b) Find the resistance of the bulb. (c) How much time can the flashlight operate before the battery goes dead? (d) What is the total charge that the battery can deliver in this time? (e) How much total energy was stored in the battery?
22. Given two resistors, R1 = 100 Ω and R2 = 470 Ω, find the equivalent resistance if connected: (a) in series and (b) in parallel.
23. Suppose a third resistor is combined with the two resistors from the previous problem in order to produce a certain desired effective resistance. For each of the following desired resistances determine the value of the third resistor and show how it should be connected with the other two: (a) 675 Ω, (b) 33.0 Ω, (c) 275 Ω.
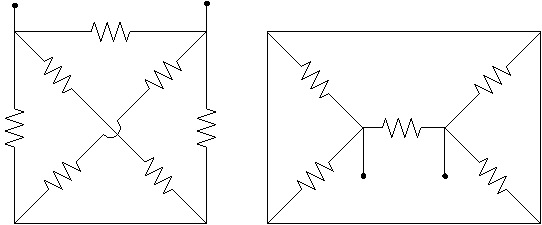
24.
Each
resistor in the diagrams below has resistance R. Find the
effective resistance between the two open terminals in terms of R for
each network of resistors shown.
(a)
(b)
25. Resistors R1 = 1.2 kΩ and R2 = 6.8 kΩ are connected in series with a 1.5 V cell in a single circuit loop. (a) Find the current. (b) Find the voltage for R1. (c) Determine the wattage of the resistor that dissipates the most energy.
26. Resistors R1 = 1.2 kΩ and R2 = 6.8 kΩ and a 1.5 V cell are all connected in parallel. (a) Find the current through the cell. (b) Find the current for R2. (c) Determine the wattage of the resistor that dissipates the most energy.
27.
Shown below
is a circuit of resistors connected to a 6.00 V battery. (a) Solve for
the current through the battery. (b) Find the voltage across the 100
Ω resistor. (c) Find the current through
the 470 Ω resistor. (d) Find the
power dissipated by the 330 Ω resistor.
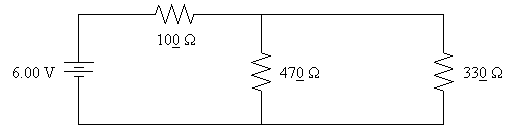
28.
Shown below
is a circuit of resistors connected to a 6.00 V battery. (a) Solve for
the current through the battery. (b) Find the voltage across the 100
Ω resistor. (c) Find the current through
the 470 Ω resistor. (d) Find the
power dissipated by the 330 Ω resistor.
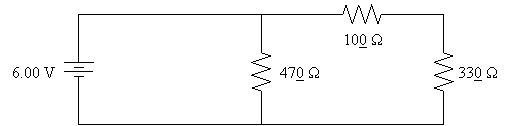
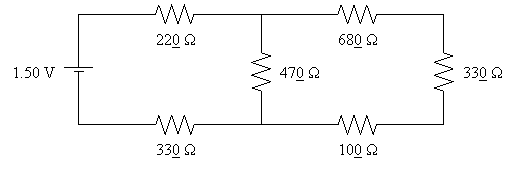
29.
Shown below
is a circuit of resistors connected to a 1.50 V cell. (a) Find the power
of the cell. (b) Determine the current for the 100 Ω resistor. (c) Determine the voltage across the 100
Ω resistor. (d) Which resistor generates
the most heat? Support your answer with words and/or calculations.
30. Suppose each network of resistors from problem #24 is connected to a voltage source. For each case, (a) and (b), determine which part of the circuit carries the greatest current and which part carries the least current. Support your answers in words or with algebraic solutions.
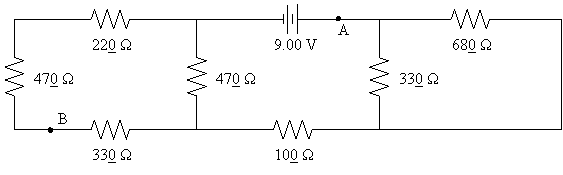
31.
Shown below
is a circuit of resistors connected to a 9.00 V battery. (a) Find the
total power dissipated by all of the resistors in the circuit. (b) Solve
for the current in the 100 Ω resistor and
describe its direction as left or right. (c) Determine the potential
difference VB -
VA.
32. Two resistors, R1 and R2, are connected in series in a certain circuit. The voltages across each resistor are: V1 = 3.0 V and V2 = 5.0 V. (a) Given that R1 = 470 Ω, what is the resistance of R2? (b) Suppose the same two resistors are connected in parallel within a circuit, what will be the ratio of the currents in each: I1/I2 = ?
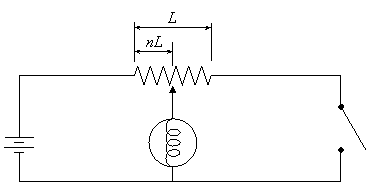
33.
A 100
Ω variable resistor (sometimes referred to as a potentiometer) is
connected to a bulb of resistance 50.0 Ω (assumed to be constant) and a
6.00 V battery as shown below. The sliding point of contact in the
variable resistor moves along the entire length of the 100 Ω
resistive element, which has a uniform cross sectional
area. Let n = fraction of the length. (a) With the switch
open, determine the power of the bulb at n = 0, 0.75, 1. (b)
Repeat with the switch closed.
34.
A certain
part of an electric circuit is shown below. Current I1
equals 0.30 A. (a) Solve for I2. (b) Solve for I3.
(c) Solve for the potential difference VB - VA.

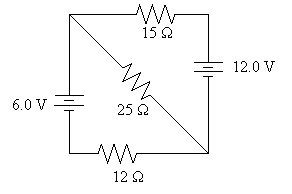
35.
For the
circuit shown below determine the following: (a) Find the current through
each battery, taking an upward direction to be positive. (b) Find the
power produced (or absorbed) by each battery. (c) Find the power of each
resistor and show that the results are consistent with conservation of energy.
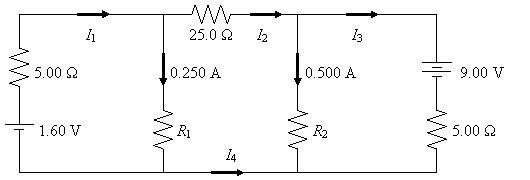
36.
Examine the
circuit shown below and solve for: (a) the four unknown currents and (b)
the two unknown resistances.
37.
Strings of
holiday lights typically consist of strands of 50 bulbs connected in series and
powered by household voltage of 120 V. The entire strand dissipates 30
W. To prevent the entire strand from going out when one bulb blows, each
bulb has a “shunting device” that allows current to flow after the
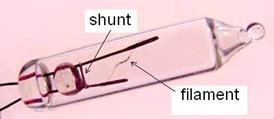
filament burns out. The shunt consists of a piece of wire with a
resistive coating that runs parallel to the filament. (a) How should the
resistance of the shunt compare to the resistance of the filament during normal
operation? Explain. (b) Determine the resistance, voltage, and
current for a single filament in normal operation. (c) What is the
voltage across the shunt just after the filament breaks? (d) The
resistive coating melts after the filament breaks (but not before) Why? (e) What is the effect, if any, on the rest of the bulbs once the shunt is
connected? Explain.
38. A light bulb of resistance R (assumed to be constant) is powered by two voltaic cells, each with voltage V and energy content U. The two cells can be connected either in series or in parallel. (a) Derive expressions for the power of the bulb in each type of connection. (b) Derive expressions for the amount of time the bulb will remain lit in each type of connection. (c) Compare and contrast the advantages and disadvantages of the two types of connections.
39. Let’s revisit the previous problem with real voltaic cells. Each cell has an emf ε = 1.55 V and internal resistance r = 0.60 Ω. Assume the bulb has constant resistance R = 30.0 Ω. (a) Find the power of the bulb with cells connected in series and with cells connected in parallel. (b) Find the efficiency of the battery in each case (i.e. efficiency with which energy from the emf’s of the cells is converted to energy emitted by the bulb).
40. Repeat problem #28, but this time assume the battery has ε = 6.00 V and internal resistance r = 3.00 Ω.
41. A certain piezoelectric buzzer requires 3.00 V and 15.0 mA current for normal operation. Design a circuit in which this device can be turned on or off and operate normally when powered by battery with ε = 6.20 V and r = 2.50 Ω. Show a circuit diagram and describe the parts needed and calculate the specifications thereof.
42. A rechargeable battery with emf 1.52 V and internal resistance 0.75 Ω is connected positive to positive and negative to negative with a 3.00 V battery with internal resistance 1.4 Ω. Assume the emf of each battery remains constant. (a) Find the current. (b) How much energy will be stored in the rechargeable battery in 1.00 minute? (c) Determine the efficiency of this charging arrangement. (d) How could the efficiency be improved (and wasted energy be reduced)? Are there any problems with improving efficiency?
43. Suppose a bulb in a flashlight has resistance R (assume it to be constant) and it is powered by a series “stack” of N identical voltaic cells each with emf ε and internal resistance r. Adding cells to the stack increases the power output of the bulb, but only to a certain extent. (a) Derive an expression for the maximum power of the bulb in terms of the given variables. Now suppose ε = 1.60, r = 0.75 Ω, and R = 40.0 Ω. (b) What is the maximum wattage of the bulb? (c) How many cells would it take to achieve 90% of the maximum wattage? (d) How does the efficiency of a flashlight change as the number of cells is increased? Explain.
44. A certain galvanometer has a resistance of 85 Ω and a full-scale current of 475 μA. Find the resistor needed and show how to connect it with this galvanometer to design the following meters: (a) a voltmeter that reads 20.0 V at full scale, and (b) an ammeter that reads 5.0 A at full scale.
45. A particular multimeter employs a 19.1 kΩ resistor in series with a galvanometer for the 0 – 2 V range and a 99.7 kΩ resistor in series with the same galvanometer for the 0 – 10 V range. (a) What is the resistance of the galvanometer? (b) What is the number of ohms per volt (full scale) of this multimeter? This is the total resistance of the voltmeter depending on which range is used. (c) In order to measure current in the 0 – 100 mA range, what shunt resistor would be required?
46. A 12.0 V battery with internal resistance 5.00 Ω is connected to a 100.0 Ω resistor. A student then uses a multimeter to measure the current and then the voltage across the resistor. (a) Find the value of the current and voltage before the meter is connected. (b) What current will be read if the resistance of the multimeter is 10.0 Ω when functioning as an ammeter? (c) What voltage will be read if the resistance of the multimeter is 10.0 kΩ when functioning as a voltmeter? (d) Calculate the percent error in each reading. (e) Would the value of the resistor influence which reading is most accurate? Explain.
1.
a. 0.26 A
b. sketch
c. 1.9 × 1019
2. 6.0 minutes
3.
a. 17 kC
b. 410 C
4. a. 50
V, 100 V, 150 V
b. 150 V, 300 V, 450 V
5. a.
0.051 Ω
b. 140 Ω
c. 0.035%
6. a.
27 mA
b. 17 V
7. a.
28 Ω, 32 Ω
b.
c.
8. a. b. c.
9. a.
0.11 Ω
b. 0.11 mm
10. a. b.
11. a. 8.02 Ω/km
b. 2.41 V
12. Al dia. = 1.26 time Cu
13. a. 9.96 × 105
Ω-1m-1
b. 1.00 × 10-6 Ωm
c. nichrome
14. a. 3.8 × 105
A/m2
b. 4.0 × 10-5 m/s
c. 10 h
d. 9.1 mV
15. a. 0.084 V/m
b. 4.8 A, 0.25 V
c. 3.6 × 10-4 m/s
16. a. 0.0167 Ω
b. 0.0063 V/m
c. 3.7 × 105 A/m2
17. a. 3.0 kW
b. 4500 J
c. 380 C
18. a. 0.8 A
b. 0.2 ns
19. a. 3.6 MJ
b. 30 kC
c. 8 A
20. a. 18 kW
b. 24 A
21. a. 0.33 A
b. 18 Ω
c. 3.6 h
d. 4300 C
e. 26 kJ
22. a. 570 Ω
b. 82.5 Ω
23. possibilities:
a. 105 Ω
b. 55.0 Ω
c. 279 Ω or 563 Ω
24. a. 4R/7
b. R/2
25. a. 0.19 mA
b. 0.23 V
c. 0.24 mW (R2)
26. a. 1.5 mA
b. 0.22 mA
c. 1.9 mW (R1)
27. a. 20.4 mA
b. 2.04 V
c. 8.42 mA
d. 47.5 mW
28. a. 26.7 mA
b. 1.40 V
c. 12.8 mA
d. 64.3 mW
29. a. 2.56 mW
b. 0.507 mA
c. 50.7 mV
d. the 330 Ω
(0.958 mW)
30. a. b.
31. a. 0.126 W
b. 14.0 mA, left
c. -5.96 V
32. a. 780 Ω
b. 1.7
33. a. 0.720 W, 0.115 W,
0.0800 W
b. 0.720 W, 0.0238 W,
0.00 W
34. a. 1.8 A
b. -1.5 A
c. -14 V
35. a. -0.070 A, 0.34 A
b. 0.42 W absorbed,
4.1 W produced
c. 1.8 W, 1.9 W,
0.059 W
36. a. 0.0743 A, -0.176 A,
-0.676 A, 0.176 A
b. 4.91 Ω, 11.2 Ω
37. a.
b. 9.6 Ω, 2.4 V, 0.25 A
c.
d.
e.
38. a. 4V 2/R,
V 2/R
b.
c.
39. a. 0.30 W, 0.079 W
b. 96%, 99%
40. a. 26.4 mA
b. 1.38 V
c. 12.6 mA
d. 62.6 mW
41. one solution uses a
211 Ω resistor
42. a. 0.69 A
b. 63 J
c. 51%
d.
43. a. Pmax = ε2R r−2
b. 180 W
c. 986
d.
44. a. 42.0 kΩ, schematic
b. 8.08 mΩ, schematic
45. a. 1050 Ω
b. 10000 Ω/V
c. 1.04 Ω
46. a. 0.114 A, 11.4 V
(11.4286)
b. 0.104 A
c. 11.4 V (11.4231)
d. 8.7%, 0.05%
e.