AP Physics Lab – Magnetic Force on a Current

Purpose

In this experiment you will use a “current balance” system to explore the various factors that govern the force that acts on a current carrying wire placed in a magnetic field. In the process of doing so you will also determine the field strength of the permanent magnets used in the apparatus.

Procedure

The permanent magnet assembly is placed on an electronic balance that can measure to the nearest 0.01 gram. The tare button on the balance sets the reading to zero. A section of wire or “current loop” is lowered into the gap of the magnet and a current is established with a variable DC power supply. The current is measured with an ammeter. Note that the “current loop” placed in the magnetic field is actually a conducting path on a small circuit board. The apparatus comes with several current loops consisting of various lengths of conducting paths for placement in the field. Two of the loops are “double lengths” – conductors on each side of the circuit board; this effectively doubles the length. The length can be determined using a ruler. The magnet assembly holds six permanent horseshoe magnets. These can be removed or replaced individually to give control over the strength of the magnetic field. Note that the U-shaped plastic “keeper” does not have to be installed when varying the number of magnets but should be returned to its original status at the end of the lab.

Parts:

Note: The current loop must not contact the magnet assembly – i.e. it must be free on all sides (but “surrounded” by the magnet).

Setup: Electrical connections:

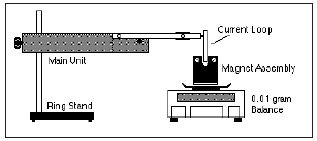
Note: the balance is calibrated to read grams, which is a properly a mass unit. However, to make the data collection and analyses more convenient the gram will be treated as a force unit since the force is directly proportional to the balance’s reading. Only in the final analyses do you need to worry about determining the force in the more proper units of newtons.

Part A – the Right Hand Rule

Use a magnetic compass to determine which side of the magnet assembly is the north pole – the red or the white. Use the right hand rule to determine which direction current should flow so that the force on the loop is upward. The result of this is that the force on the magnet should be downward and cause the scale to have a positive reading (it is designed to respond to a downward push). Complete the diagram on the data page by sketching and labeling the correct orientation of the magnet’s poles (grey represents red) and the magnetic field between the poles and around the outside of the magnet. Also show the current’s direction through the magnetic field that will result in a downward force on the balance. Use the equipment to confirm the features of your sketch.

Part B – Force vs. Current (constant length and field)

Use the longest “single length” current loop (part #SF 38). Record the length of the part of the loop that resides in the field. Vary the current and measure the resulting force.

Part C – Force vs. Length (constant current and field)

Using the same current each time, measure the resulting force on each of the six current loops. Adjust the current to 3.00 A for each trial. Record length and force. Note that parts #SF 41 and #SF 42 are “double lengths” in which the current “loops around” and passes through the field twice – record a single value for length that is equal to twice the length measured on one side.

Part D – Force vs. Number of Magnets (constant current and length).

Use the current loop of your choice. (Which do you think would be best for this?) Record the length. Use the same current each time: 3.00 A. Measure the force with all six magnets. Then remove one magnet at a time and record each resulting force. (How should the remaining magnets be arranged to get the most uniform field?)

Analyses

For parts B, C, and D produce appropriate, well-labeled graphs, including line or curve of best fit and corresponding regression equation.

Questions

1. Explain how the results of the lab support or refute the equation for finding the magnetic force on a current carrying wire. Be specific and refer to the graphs, tables, diagram, etc.

2. (a) Use the slope from the Force vs. Current graph and the length of the current loop to determine the strength of the magnetic field in teslas (you will need to change grams to newtons). Show all work. (b) Use the slope from the Force vs. Length graph and the current to determine the strength of the magnetic field in teslas. Show all work. (c) Determine the percent difference in the two values.

3. Consider the graph of Force vs. Number of Magnets. Theoretically, should this graph be linear? Support and explain your answer. Your response should demonstrate your understanding of the field of a permanent magnet and the superposition principle.

4. Explain the physics principle that allows us to conclude that the force acting on the current loop has the same magnitude as the force measured by the scale (the apparent weight of the magnet assembly).

5. Discuss error.

Data/Observations:

Part A – Right Hand Rule

Overhead view of magnet assembly and current loop:

(Label poles, sketch and label magnetic field, sketch and label current and its direction.)

Part B – Force vs. Current		Part C – Force vs. Length		Part D - Force vs. Number of Magnets
Length =		Current =		Current =
# of Magnets =		# of Magnets =		Length =
Current (A)	Force (g)	Length (cm)	Force (g)	Number of Magnets	Force (g)